
【题目】以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系.
(1)将直线l: 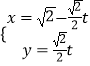 (t为参数)化为极坐标方程;
(t为参数)化为极坐标方程;
(2)设P是(1)中直线l上的动点,定点A( ![]() ,
, ![]() ),B是曲线ρ=﹣2sinθ上的动点,求|PA|+|PB|的最小值.
),B是曲线ρ=﹣2sinθ上的动点,求|PA|+|PB|的最小值.
【答案】
(1)解:由直线l: 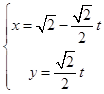 (t为参数)消去参数t,可得x+y=
(t为参数)消去参数t,可得x+y= ![]() ,化为极坐标方程ρcosθ+ρsinθ=
,化为极坐标方程ρcosθ+ρsinθ= ![]()
(2)解:定点A( ![]() ,
, ![]() ),化为A(1,1).
),化为A(1,1).
曲线ρ=﹣2sinθ化为ρ2=﹣2ρsinθ,∴直角坐标方程为:x2+y2=﹣2y,
配方为x2+(y+1)2=1.
可得圆心C(0,﹣1).
连接AC交直线l于点P,交⊙C于点B,
|AC|= ![]() =
= ![]() ,
,
∴|PA|+|PB|的最小值=|AC|﹣r= ![]() ﹣1.
﹣1.

【解析】(1)由直线l:  (t为参数)消去参数t,可得x+y=
(t为参数)消去参数t,可得x+y= ![]() ,利用
,利用 ![]() 即可化为极坐标方程;(2)定点A(
即可化为极坐标方程;(2)定点A( ![]() ,
, ![]() ),化为A(1,1).曲线ρ=﹣2sinθ化为ρ2=﹣2ρsinθ,可得直角坐标方程:x2+(y+1)2=1.可得圆心C(0,﹣1).连接AC交直线l于点P,交⊙C于点B,可得|PA|+|PB|的最小值=|AC|﹣r.
),化为A(1,1).曲线ρ=﹣2sinθ化为ρ2=﹣2ρsinθ,可得直角坐标方程:x2+(y+1)2=1.可得圆心C(0,﹣1).连接AC交直线l于点P,交⊙C于点B,可得|PA|+|PB|的最小值=|AC|﹣r.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx,g(x)=﹣x2+ax﹣2
(Ⅰ)求函数f(x)在[t,t+2](t>0)上的最小值;
(Ⅱ)若函数y=f(x)与y=g(x)的图象恰有一个公共点,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
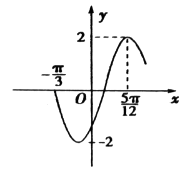
【题目】函数f(x)=Asin(ωx+φ),x∈R,(ω>0,﹣ ![]() <φ<
<φ< ![]() )的部分图象如图所示.
)的部分图象如图所示.
(Ⅰ)确定A,ω,φ的值,并写出函数f(x)的解析式;
(Ⅱ)描述函数y=f(x)的图象可由函数y=sinx的图象经过怎样的变换而得到;
(Ⅲ)若f( ![]() )=
)= ![]() (
( ![]() <α<
<α< ![]() ),求tan2(α﹣
),求tan2(α﹣ ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学餐饮中心为了了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
(1)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(2)已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率. 附:K2= ![]()
P(K2>k0) | 0.10 | 0.05 |
| 0.005 |
k0 | 2.706 | 3.841 |
| 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体ABCD﹣A1B1C1D1中,AA1=2AB=2BC,E,F,E1分别是棱AA1 , BB1 , A1B1的中点. 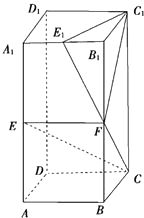
(1)求证:CE∥平面C1E1F;
(2)求证:平面C1E1F⊥平面CEF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() (其中ω>0)
(其中ω>0)
(I)求函数f(x)的值域;
(II)若对任意的a∈R,函数y=f(x),x∈(a,a+π]的图象与直线y=﹣1有且仅有两个不同的交点,试确定ω的值(不必证明),并求函数y=f(x),x∈R的单调增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线 ![]() 上的一点
上的一点 ![]() 的横坐标为
的横坐标为 ![]() ,焦点为
,焦点为 ![]() ,且
,且 ![]() ,直线
,直线 ![]() 与抛物线
与抛物线 ![]() 交于
交于 ![]() 两点.
两点.
(1)求抛物线 ![]() 的方程;
的方程;
(2)若 ![]() 是
是 ![]() 轴上一点,且△
轴上一点,且△ ![]() 的面积等于
的面积等于 ![]() ,求点
,求点 ![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com