
 .
. (
( +1),Sn=b1+b2+…+bn,Tn=S1+S2+…+Sn,试用S2011 表示T2011.
+1),Sn=b1+b2+…+bn,Tn=S1+S2+…+Sn,试用S2011 表示T2011. 可得此方程没有实数根,故数列{an}中不存在三项成等差数列.
可得此方程没有实数根,故数列{an}中不存在三项成等差数列. -(q-
-(q- )2],结合[
)2],结合[ -(q+
-(q+ )2]∈(
)2]∈( ,1)讨论可得只有ak-(ak+1+ak+2)=ak+1,得到方程q2+2q-1=0解之得q=
,1)讨论可得只有ak-(ak+1+ak+2)=ak+1,得到方程q2+2q-1=0解之得q= (舍负);
(舍负); ,从而得到Sn=1+
,从而得到Sn=1+ +
+ +…+
+…+ ,进而得到Tn=1+(1+
,进而得到Tn=1+(1+ )+(1+
)+(1+ +
+ )+…+(1+
)+…+(1+ +
+ +…+
+…+ ),对此式重新组合整理得Tn=(n+1)Sn-n,由此将n=2011代入即可得到用S2011 表示T2011的式子.
),对此式重新组合整理得Tn=(n+1)Sn-n,由此将n=2011代入即可得到用S2011 表示T2011的式子. .
. -(q-
-(q- )2]
)2] -(q+
-(q+ )2]∈(
)2]∈( ,1),
,1), (舍负);
(舍负); ,
, )n-1,可得bn=-log
)n-1,可得bn=-log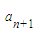 (
( +1)=
+1)= =
= ,
, +
+ +…+
+…+ ,
, )+(1+
)+(1+ +
+ )+…+(1+
)+…+(1+ +
+ +…+
+…+ )
) (n-1)+
(n-1)+ (n-2)+…+
(n-2)+…+ [n-(n-1)]=n(1+
[n-(n-1)]=n(1+ +
+ +…+
+…+ )-(
)-( +
+ +…+
+…+ )
) )+(1-
)+(1- )+…+(1-
)+…+(1- )]=nSn-[(n-1)-(
)]=nSn-[(n-1)-( +
+ +…+
+…+ )]
)] +
+ +…+
+…+ )]=nSn-n+Sn=(n+1)Sn-n
)]=nSn-n+Sn=(n+1)Sn-n 的正项等比数列,讨论它的某三项成等差数列,求数列的通项公式并依此解决数列{bn}的前n项和的问题.着重考查了等差数列、等比数列的通项公式与求和公式,以及数列与函数的综合等知识,属于中档题.
的正项等比数列,讨论它的某三项成等差数列,求数列的通项公式并依此解决数列{bn}的前n项和的问题.着重考查了等差数列、等比数列的通项公式与求和公式,以及数列与函数的综合等知识,属于中档题. 

科目:高中数学 来源:2011届本溪县高二暑期补课阶段考试数学卷 题型:解答题
(本题满分12分)已知各项均为正数的数列 ,
, 的等比中项。
的等比中项。
(1)求证:数列 是等差数列;(2)若
是等差数列;(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省石家庄高三上学期调研考试文科数学试卷(解析版) 题型:选择题
已知各项均为正数的等比数列 中,
中, 与
与 的等比中项为
的等比中项为 ,则
,则 的最小值为( )
的最小值为( )
A.16 B.8 C. D.4
D.4
查看答案和解析>>
科目:高中数学 来源:2013届辽宁朝阳柳城高中高三上第三次月考理科数学试卷(解析版) 题型:解答题
已知各项均为正数的数列 ,
,
 的等比中项。
的等比中项。
(1)求证:数列 是等差数列;(2)若
是等差数列;(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。
查看答案和解析>>
科目:高中数学 来源:2013届辽宁朝阳柳城高中高三上第三次月考文科数学试卷(解析版) 题型:解答题
(12分)已知各项均为正数的数列 ,
,
 的等比中项。
的等比中项。
(1)求证:数列 是等差数列;
是等差数列;
(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年本溪县高二暑期补课阶段考试数学卷 题型:解答题
(本题满分12分)已知各项均为正数的数列 ,
,
 的等比中项。
的等比中项。
(1)求证:数列 是等差数列;(2)若
是等差数列;(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com