
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,证明
时,证明![]() ;
;
(2)当![]() 时,对于两个不相等的实数
时,对于两个不相等的实数![]() 、
、![]() 有
有![]() ,求证:
,求证:![]() .
.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)a=1时,对f(x)求导,判断f(x)单调性求出它的最小值即可证明。
(2)先判断函数f(x)的单调区间,再构造![]() ,求导判断它的单调性,根据
,求导判断它的单调性,根据![]() ,且
,且![]() ,可得
,可得![]() 不在同一个单调区间内,不妨设
不在同一个单调区间内,不妨设![]() ,利用函数的单调性即可证明.
,利用函数的单调性即可证明.
(1)∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
∴![]() 时,
时,![]() 取得极小值,即最小值
取得极小值,即最小值![]() .
.
即![]() .
.
(2)证明:当![]() 时,
时,![]() ,
,
则![]() ,∴
,∴![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
令![]() ,
,
则![]() ,∴
,∴![]() .
.
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,![]() 单调递减,
单调递减,
∴![]() ,即
,即![]() ,
,
∴当![]() 时,
时,![]() .
.
又![]() 在
在![]() 内是增函数,在
内是增函数,在![]() 内是减函数.
内是减函数.
又∵![]() ,且
,且![]() ,∴
,∴![]() ,
,![]() 不在同一单调区间内,
不在同一单调区间内,
不妨设![]() ,由上可知:
,由上可知:![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() ,
,![]() ,又
,又![]() 在
在![]() 内是增函数,∴
内是增函数,∴![]() ,即
,即![]() .
.


科目:高中数学 来源: 题型:
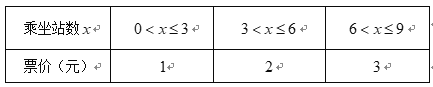
【题目】某城市为鼓励人们绿色出行,乘坐地铁,地铁公司决定按照乘客经过地铁站的数量实施分段优惠政策,不超过![]() 站的地铁票价如下表:现有甲、乙两位乘客同时从起点乘坐同一辆地铁,已知他们乘坐地铁都不超过
站的地铁票价如下表:现有甲、乙两位乘客同时从起点乘坐同一辆地铁,已知他们乘坐地铁都不超过![]() 站,且他们各自在每个站下车的可能性是相同的.
站,且他们各自在每个站下车的可能性是相同的.
(1)若甲、乙两人共付费![]() 元,则甲、乙下车方案共有多少种?
元,则甲、乙下车方案共有多少种?
(2)若甲、乙两人共付费![]() 元,求甲比乙先到达目的地的概率.
元,求甲比乙先到达目的地的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了解用户对其产品的满意度,从某地区随机调查了100个用户,得到用户对产品的满意度评分频率分布表如下:
组别 | 分组 | 频数 | 频率 |
第一组 |
| 10 | 0.1 |
第二组 |
| 20 | 0.2 |
第三组 |
| 40 | 0.4 |
第四组 |
| 25 | 0.25 |
第五组 |
| 5 | 0.05 |
合计 | 100 | 1 |
(1)根据上面的频率分布表,估计该地区用户对产品的满意度评分超过70分的概率;
(2)请由频率分布表中数据计算众数、中位数,平均数,根据样本估计总体的思想,若平均分低于75分,视为不满意.判断该地区用户对产品是否满意?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数y=H(x),若在其定义域内存在x0,使得x0·H(x0)=1成立,则称x0为函数H(x)的“倒数点”.已知函数f(x)=ln x,g(x)=![]() (x+1)2-1.
(x+1)2-1.
(1)求证:函数f(x)有“倒数点”,并讨论函数f(x)的“倒数点”的个数;
(2)若当x≥1时,不等式xf(x)≤m[g(x)-x]恒成立,试求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系中,以原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() :
:![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 、
、![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)求线段![]() 的长和
的长和![]() 的积.
的积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学习合作小组学习了祖暅原理:“幂势既同,则积不容异”,意思是夹在两个平行平面间的两个几何体,被平行于这两个平行平面的任何平面所截,如果截得两个截面的面积总相等,那么这两个几何体的体积相等.利用祖暅原理研究椭圆![]() 绕
绕![]() 轴旋转一周所得到的椭球体的体积,方法如下:取一个底面圆半径为
轴旋转一周所得到的椭球体的体积,方法如下:取一个底面圆半径为![]() 高为
高为![]() 的圆柱,从圆柱中挖去一个以圆柱上底面为底面,下底面圆心为顶点的圆锥,把所得的几何体和半椭球体放在同一平面
的圆柱,从圆柱中挖去一个以圆柱上底面为底面,下底面圆心为顶点的圆锥,把所得的几何体和半椭球体放在同一平面![]() 上,那么这两个几何体也就夹在两个平行平面之间了,现在用一平行于平面
上,那么这两个几何体也就夹在两个平行平面之间了,现在用一平行于平面![]() 的任意一个平面
的任意一个平面![]() 去截这两个几何体,则截面分别是圆面和圆环面,经研究,圆面面积和圆环面面积相等,由此得到椭球体的体积是__________.
去截这两个几何体,则截面分别是圆面和圆环面,经研究,圆面面积和圆环面面积相等,由此得到椭球体的体积是__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《郑州市城市生活垃圾分类管理办法》已经政府常务会议审议通过,自2019年12月1日起施行.垃圾分类是对垃圾收集处置传统方式的改革,是对垃圾进行有效处置的一种科学管理方法.所谓垃圾其实都是资源,当你放错了位置时它才是垃圾.某企业在市科研部门的支持下进行研究,把厨余垃圾加工处理为一种可销售的产品.已知该企业每周的加工处理量最少为75吨,最多为100吨.周加工处理成本y(元)与周加工处理量x(吨)之间的函数关系可近似地表示为![]() ,且每加工处理一吨厨余垃圾得到的产品售价为16元.
,且每加工处理一吨厨余垃圾得到的产品售价为16元.
(Ⅰ)该企业每周加工处理量为多少吨时,才能使每吨产品的平均加工处理成本最低?
(Ⅱ)该企业每周能否获利?如果获利,求出利润的最大值;如果不获利,则需要市政府至少补贴多少元才能使该企业不亏损?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com