
【题目】在平面直角坐标系xOy中,已知曲线C的参数方程为![]() (α为参数,直线l:y=kx(k>0),以O为极点,x轴正半轴为极轴建立极坐标系.
(α为参数,直线l:y=kx(k>0),以O为极点,x轴正半轴为极轴建立极坐标系.
(Ⅰ)求曲线C的极坐标方程;
(Ⅱ)若直线l与曲线C交于A,B两点,求|OA||OB|的值.
【答案】(Ⅰ)ρ2-2ρcosθ-3=0(Ⅱ)3
【解析】
(Ⅰ)利用同角的三角函数关系式,把曲线C的参数方程化为普通方程,再利用
公式,化成极坐标方程;
(Ⅱ)把直线化成极坐标方程代入圆的极坐标方程中,根据一元二次方程的根与系数的关系和极径的几何意义求出。
解:(Ⅰ)由曲线C的参数方程消去参数α可得曲线C的普通方程为:(x-1)2+y2=4,即x2+y2-2x-3=0,化为极坐标方程为ρ2-2ρcosθ-3=0.
(Ⅱ)直线l的极坐标方程为θ=β(β∈(0,![]() )),
)),
将θ=β代入方程ρ2-2ρcosθ-3=0,得ρ2-2ρcosβ-3=0,∴ρ1ρ2=-3,
∴|OA||OB|=|ρ1ρ2|=3.


 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
【题目】早在一千多年之前,我国已经把溢流孔用于造桥技术,以减轻桥身重量和水流对桥身的冲击,现设桥拱上有如图所示的4个溢流孔,桥拱和溢流孔轮廓线均为抛物线的一部分,且四个溢流孔轮廓线相同.根据图上尺寸,在平面直角坐标系![]() 中,桥拱所在抛物线的方程为_______,溢流孔与桥拱交点
中,桥拱所在抛物线的方程为_______,溢流孔与桥拱交点![]() 的坐标为_______.
的坐标为_______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】历史上数列的发展,折射出许多有价值的数学思想方法,对时代的进步起了重要的作用,比如意大利数学家列昂纳多·斐波那契以兔子繁殖为例,引入“兔子数列”:即1,1,2,3,5,8,13,21,34,55,89,144,233,….即![]() ,
,![]() ,此数列在现代物理、准晶体结构及化学等领域有着广泛的应用,若此数列被4整除后的余数构成一个新的数列
,此数列在现代物理、准晶体结构及化学等领域有着广泛的应用,若此数列被4整除后的余数构成一个新的数列![]() ,又记数列
,又记数列![]() 满足
满足![]() ,
,![]() ,
,![]() ,则
,则![]() 的值为_____.
的值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知抛物线C:x2=4y的焦点为F,直线l与抛物线C交于A,B两点,延长AF交抛物线C于点D,若AB的中点纵坐标为|AB|-1,则当∠AFB最大时,|AD|=( )
A. 4B. 8C. 16D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
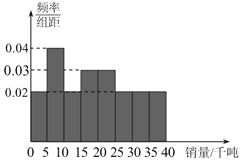
【题目】为了打好“精准扶贫攻坚战”某村扶贫书记打算带领该村农民种植新品种蔬菜,可选择的种植量有三种:大量种植,适量种植,少量种植.根据收集到的市场信息,得到该地区该品种蔬菜年销量频率分布直方图如图,然后,该扶贫书记同时调查了同类其他地区农民以往在各种情况下的平均收入如表1(表中收入单位:万元):
表1
销量 种植量 | 好 | 中 | 差 |
大量 |
| 8 | -4 |
适量 | 9 | 7 | 0 |
少量 | 4 | 4 | 2 |
但表格中有一格数据被墨迹污损,好在当时调查的数据频数分布表还在,其中大量种植的100户农民在市场销量好的情况下收入情况如表2:
收入(万元) | 11 | 11.5 | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 |
频数(户) | 5 | 10 | 15 | 10 | 15 | 20 | 10 | 10 | 5 |
(Ⅰ)根据题中所给数据,请估计在市场销量好的情况下,大量种植的农民每户的预期收益.(用以往平均收入来估计);
(Ⅱ)若该地区年销量在10千吨以下表示销量差,在10千吨至30千吨之间表示销量中,在30千吨以上表示销量好,试根据频率分布直方图计算销量分别为好、中、差的概率(以频率代替概率);
(Ⅲ)如果你是这位扶贫书记,请根据(Ⅰ)(Ⅱ),从农民预期收益的角度分析,你应该选择哪一种种植量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知棱柱![]() 的底面是菱形,且
的底面是菱形,且![]() 面ABCD,
面ABCD,![]() ,F为棱
,F为棱![]() 的中点,M为线段
的中点,M为线段![]() 的中点.
的中点.

(1)求证:![]() 面ABCD;
面ABCD;
(2)判断直线MF与平面![]() 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(3)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,焦距为6.
,焦距为6.
(1)求椭圆![]() 的方程.
的方程.
(2)过椭圆左顶点的两条斜率之积为![]() 的直线分别与椭圆交于
的直线分别与椭圆交于![]() 点.试问直线
点.试问直线![]() 是否过某定点?若过,求出该点的坐标;若不过,请说明理由.
是否过某定点?若过,求出该点的坐标;若不过,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在梯形![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,线段
的中点,线段![]() 与
与![]() 交于
交于![]() 点(如图1).将
点(如图1).将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得二面角
的位置,使得二面角![]() 为直二面角(如图2).
为直二面角(如图2).
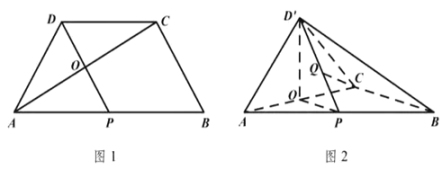
(1)求证:![]() 平面
平面![]() ;
;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com