
分析 (1)设抛物线的方程为y2=2px,把A点的坐标$({\frac{1}{2},-\sqrt{2}})$代入方程,求解即可.
(2)直线l的方程为y-1=k(x+2),即y=kx+2k+1,联立方程组$\left\{{\begin{array}{l}{y=kx+2k+1}\\{{y^2}=4x}\end{array}}\right.$,消去x,化简得ky2-4y+4(2k+1)=0,①当k=0,求解直线与抛物线有一个公共点$({\frac{1}{4},1})$,②当k≠0,通过$\left\{{\begin{array}{l}{k≠0}\\{△={{({-4})}^2}-4k•4({2k+1})≥0}\end{array}}\right.$
求解k的范围即可.
解答 解:(1)依题意设抛物线的方程为y2=2px,
把A点的坐标$({\frac{1}{2},-\sqrt{2}})$代入方程得${({-\sqrt{2}})^2}=2p×\frac{1}{2}$,
解得p=2∴抛物线的标准方程y2=4x;
(2)直线l的方程为y-1=k(x+2),即y=kx+2k+1
解联立方程组$\left\{{\begin{array}{l}{y=kx+2k+1}\\{{y^2}=4x}\end{array}}\right.$,消去x,
得${y^2}=\frac{4}{k}({y-2k-1})$,化简得ky2-4y+4(2k+1)=0
①当k=0,代入ky2-4y+4(2k+1)=0得y=1代入y2=4x,得$x=\frac{1}{4}$
这时直线与抛物线有一个公共点$({\frac{1}{4},1})$,
②当k≠0,依题意得$\left\{{\begin{array}{l}{k≠0}\\{△={{({-4})}^2}-4k•4({2k+1})≥0}\end{array}}\right.$
解得-1≤k<0或$0<k≤\frac{1}{2}$
综合①②,当$-1≤k≤\frac{1}{2}$时直线与抛物线有公共点.
点评 本题考查直线与抛物线的位置关系的应用,抛物线方程的求法,考查计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 1 | C. | -1 | D. | -$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
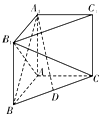 如图,在三棱柱ABC-A1B1C1中,A1A⊥平面ABC,AB⊥AC,AB=AC=AA1,D为BC的中点.
如图,在三棱柱ABC-A1B1C1中,A1A⊥平面ABC,AB⊥AC,AB=AC=AA1,D为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com