已知:f(x)=lg(ax-bx)(a>1>b>0).
(1)求f(x)的定义域;
(2)判断f(x)在其定义域内的单调性;
(3)若f(x)在(1,+∞)内恒为正,试比较a-b与1的大小.
解:(1)要使函数有意义,则a
x-b
x>0,∴
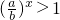
,
∵
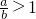
,∴x>0,∴f(x)的定义域为(0,+∞).
(2)设x
2>x
1>0,∵a>1>b>0,
∴
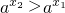
,

,则
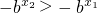
,
∴
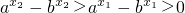
,∴
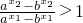
.
∵函数y=lgx在定义域上是增函数,
∴f(x
2)-f(x
1)>0,即f(x
2)>f(x
1),
∴f(x)在(0,+∞)是增函数.
(3)由(2)知,函数f(x)在(0,+∞)是增函数,
∴f(x)在(1,+∞)是增函数,即有f(x)>f(1),
要使f(x)>0恒成立,必须函数的最小值f(1)≥0,
即lg(a-b)≥0=lg1,则a-b≥1.
分析:(1)由对数的真数大于零得,a
x-b
x>0,再由a>1>b>0和指数函数的性质,求出不等式解集即函数的定义域;
(2)先在定义域任取两个自变量,即x
2>x
1>0,利用指数函数的性质比较对应真数的大小,再根据y=lgx在定义域上是增函数,得出f(x
2)与f(x
1)的大小,判断出此函数的单调性;
(3)根据(2)证出的函数单调性,求出此区间内的函数的最小值f(1),只要f(1)≥0成立即可,代入函数解析式,利用lg1=0判断a-b与1的大小.
点评:本题是关于对数型复合函数的综合题,根据真数大于零求函数的定义域,判断函数的单调性即比较真数的大小,对于恒成立问题,就是由函数的单调性求出在区间上的最值.

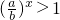 ,
,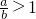 ,∴x>0,∴f(x)的定义域为(0,+∞).
,∴x>0,∴f(x)的定义域为(0,+∞).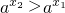 ,
, ,则
,则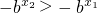 ,
,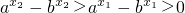 ,∴
,∴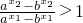 .
.

 阅读快车系列答案
阅读快车系列答案