
【题目】我国![]() 年新年贺岁大片《流浪地球》自上映以来引发了社会的广泛关注,受到了观众的普遍好评.假设男性观众认为《流浪地球》好看的概率为
年新年贺岁大片《流浪地球》自上映以来引发了社会的广泛关注,受到了观众的普遍好评.假设男性观众认为《流浪地球》好看的概率为![]() ,女性观众认为《流浪地球》好看的概率为
,女性观众认为《流浪地球》好看的概率为![]() .某机构就《流浪地球》是否好看的问题随机采访了
.某机构就《流浪地球》是否好看的问题随机采访了![]() 名观众(其中
名观众(其中![]() 男
男![]() 女).
女).
(1)求这![]() 名观众中女性认为好看的人数比男性认为好看的人数多的概率;
名观众中女性认为好看的人数比男性认为好看的人数多的概率;
(2)设![]() 表示这
表示这![]() 名观众中认为《流浪地球》好看的人数,求
名观众中认为《流浪地球》好看的人数,求![]() 的分布列.
的分布列.
科目:高中数学 来源: 题型:
【题目】如图所示的几何体,底面ABFE是边长为2的正方形,DE与CF均垂直于平面ABFE,且![]() .
.
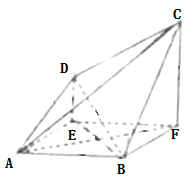
(1)证明:BE∥平面ACD;
(2)求三棱锥B﹣ACD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校想了解高二数学成绩在学业水平考试中的情况,从中随机抽出![]() 人的数学成绩作为样本并进行统计,频率分布表如下表所示.
人的数学成绩作为样本并进行统计,频率分布表如下表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
|
|
|
第2组 |
|
|
|
第3组 |
|
|
|
第4组 |
|
|
|
第5组 |
|
|
|
合计 |
|
| |
(1)据此估计这次参加数学考试的高二学生的数学平均成绩;
(2)从这五组中抽取![]() 人进行座谈,若抽取的这
人进行座谈,若抽取的这![]() 人中,恰好有
人中,恰好有![]() 人成绩为
人成绩为![]() 分,
分,![]() 人成绩为
人成绩为![]() 分,
分,![]() 人成绩为
人成绩为![]() 分,
分,![]() 人成绩为
人成绩为![]() 分,求这
分,求这![]() 人数学成绩的方差;
人数学成绩的方差;
(3)从![]() 人的样本中,随机抽取测试成绩在
人的样本中,随机抽取测试成绩在![]() 内的两名学生,设其测试成绩分别为
内的两名学生,设其测试成绩分别为![]() ,
,![]() .
.
(i)求事件“![]() ”的概率;
”的概率;
(ii)求事件“![]() ”的概率.
”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△OAB中,顶点A的坐标是(3,0),顶点B的坐标是(1,2),记△OAB位于直线![]() 左侧图形的面积为f(t).
左侧图形的面积为f(t).

(1)求函数f(t)的解析式;
(2)设函数![]() ,求函数
,求函数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为棱
为棱![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 上一动点.
上一动点.

(Ⅰ)求证:当点![]() 为线段
为线段![]() 的中点时,
的中点时,![]() 平面
平面![]() ;
;
(Ⅱ)设![]() ,试问:是否存在实数
,试问:是否存在实数![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() ?若存在,求出这个实数
?若存在,求出这个实数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合![]() ,若
,若![]() 是
是![]() 的子集,把
的子集,把![]() 中的所有数的和称为
中的所有数的和称为![]() 的“容量”(规定空集的容量为0),若
的“容量”(规定空集的容量为0),若![]() 的容量为奇(偶)数,则称
的容量为奇(偶)数,则称![]() 为
为![]() 的奇(偶)子集,命题①:
的奇(偶)子集,命题①:![]() 的奇子集与偶子集个数相等;命题②:当
的奇子集与偶子集个数相等;命题②:当![]() 时,
时,![]() 的所有奇子集的容量之和与所有偶子集的容量之和相等,则下列说法正确的是( )
的所有奇子集的容量之和与所有偶子集的容量之和相等,则下列说法正确的是( )
A.命题①和命题②都成立B.命题①和命题②都不成立
C.命题①成立,命题②不成立D.命题①不成立,命题②成立
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 对任意
对任意![]() 满足
满足![]() ,下面给出关于数列
,下面给出关于数列![]() 的四个命题:①
的四个命题:①![]() 可以是等差数列,②
可以是等差数列,②![]() 可以是等比数列;③
可以是等比数列;③![]() 可以既是等差又是等比数列;④
可以既是等差又是等比数列;④![]() 可以既不是等差又不是等比数列;则上述命题中,正确的个数为( )
可以既不是等差又不是等比数列;则上述命题中,正确的个数为( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com