
分析 (Ⅰ)设点M(x,y),依题意知N(0,y),利用$\overrightarrow{AM}•\overrightarrow{BM}=\overrightarrow{ON}•\overrightarrow{CM}$得x2-1+y2=y(y+1),即可求曲线T的方程;
(Ⅱ)求出点Q的坐标为$(\frac{4x_0^2-1}{{8{x_0}}},-\frac{5}{4})$,假设以PQ为直径的圆恒过定点H,则根据对称性,点H必在y轴上,设H(0,t),则由$\overrightarrow{PH}•\overrightarrow{QH}=0$得结论.
解答 解:(Ⅰ)设点M(x,y),依题意知N(0,y),
∵$\overrightarrow{AM}=(x+1,y),\overrightarrow{BM}=(x-1,y),\overrightarrow{ON}=(0,y),\overrightarrow{CM}=(x,y+1)$,---------------------------(2分)
由$\overrightarrow{AM}•\overrightarrow{BM}=\overrightarrow{ON}•\overrightarrow{CM}$得x2-1+y2=y(y+1),即y=x2-1,
∴所求曲线T的方程为y=x2-1-------------------(4分)
(Ⅱ)设P(x0,y0)(x0≠0),由y=x2-1,得y'=2x
则${k_l}=y'{|_{x={x_0}}}=2{x_0}$------------------------------------------------------------------------------------------(5分)
∴直线l的方程为:y-y0=2x0(x-x0)
令$y=-\frac{5}{4}$得$x=\frac{4x_0^2-1}{{8{x_0}}}$,即点Q的坐标为$(\frac{4x_0^2-1}{{8{x_0}}},-\frac{5}{4})$------------------------------------------(6分)
假设以PQ为直径的圆恒过定点H,则根据对称性,点H必在y轴上,设H(0,t),
则由$\overrightarrow{PH}•\overrightarrow{QH}=0$得${x_0}•\frac{4x_0^2-1}{{8{x_0}}}+(t-{y_0})(t+\frac{5}{4})=0$------①--------------------------------------(8分)$\frac{1}{2}{y_0}+\frac{3}{8}+t(t+\frac{5}{4})-{y_0}(t+\frac{5}{4})=0$,$(t+\frac{3}{4})(t+\frac{1}{2}-{y_0})=0$,
∴$t=-\frac{3}{4}$,即以PQ为直径的圆恒过定点,该点的坐标为$(0,-\frac{3}{4})$--------------------------(12分)】
点评 本题考查轨迹方程,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | y=cos2x-sin2x | B. | y=sin2x+cos2x | C. | y=cos2x-sin2x | D. | y=sin2x+cosx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
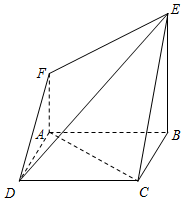 在如图所示的几何体中,四边形ABCD为正方形,四边形ABEF为直角梯形,且AF∥BE,AB⊥BE,平面ABCD∩平面ABEF=AB,AB=BE=2AF=2.
在如图所示的几何体中,四边形ABCD为正方形,四边形ABEF为直角梯形,且AF∥BE,AB⊥BE,平面ABCD∩平面ABEF=AB,AB=BE=2AF=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$ | B. | $\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}$ | C. | $\frac{4}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$ | D. | $\frac{2}{3}\overrightarrow{AB}+\frac{5}{3}\overrightarrow{AC}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
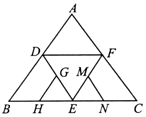 如图是正四面体的平面展开图,G,H,M,N分别为DE,BE,EF,EC的中点,在这个正四面体中,有以下结论:
如图是正四面体的平面展开图,G,H,M,N分别为DE,BE,EF,EC的中点,在这个正四面体中,有以下结论:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com