
【题目】在△ABC中,角A、B、C所对的边分别为a,b,c.已知a+c=3 ![]() ,b=3.
,b=3.
(1)求cosB的最小值;
(2)若 ![]() =3,求A的大小.
=3,求A的大小.
【答案】
(1)解:在△ABC中,由余弦定理得cosB= ![]() =
= ![]() =
= ![]() .
.
∵ac≤( ![]() )2=
)2= ![]() .
.
∴当ac= ![]() 时,cosB取得最小值
时,cosB取得最小值 ![]() .
.
(2)解:由余弦定理得b2=a2+c2﹣2accosB.
∵ ![]() accosB=3.
accosB=3.
∴9=a2+c2﹣6,∴a2+c2=15.
又∵a+c=3 ![]() ,∴ac=6.
,∴ac=6.
∴a=2 ![]() ,c=
,c= ![]() 或a=
或a= ![]() ,c=2
,c=2 ![]() .
.
∴cosB= ![]() ,sinB=
,sinB= ![]() .
.
由正弦定理得 ![]() ,
,
∴sinA= ![]() =1或
=1或 ![]() .
.
∴A= ![]() 或A=
或A= ![]()
【解析】(1)根据基本不等式求出ac的最大值,利用余弦定理得出cosB的最小值;(2)利用余弦定理列方程解出a,c,cosB,使用正弦定理得出sinA.
【考点精析】本题主要考查了正弦定理的定义和余弦定理的定义的相关知识点,需要掌握正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】某人租用一块土地种植一种瓜类作物,租期5年,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg.当年产量低于450kg时,单位售价为12元/kg,当年产量不低于450kg时,单位售价为10元/kg. 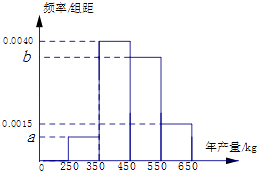
(1)求图中a的值;
(2)以各区间中点值作为该区间的年产量,并以年产量落入该区间的频率作为年产量取该区间中点值的概率,求年销售额X(单位:元)的分布列;
(3)求在租期5年中,至少有2年的年销售额不低于5000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,在△ABC中,已知AB=15,BC=14,CA=13.将△ABC沿BC边上的高AD折成一个如图②所示的四面体A﹣BCD,使得图②中的BC=11. 
(1)求二面角B﹣AD﹣C的平面角的余弦值;
(2)在四面体A﹣BCD的棱AD上是否存在点P,使得 ![]() =0?若存在,请指出点P的位置;若不存在,请给出证明.
=0?若存在,请指出点P的位置;若不存在,请给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知圆C1:x2+y2=4,圆C2:(x﹣2)2+y2=4.
(1)在以O为极点,x轴正半轴为极轴的极坐标系中,分别求圆C1与圆C2的极坐标方程及两圆交点的极坐标;
(2)求圆C1与圆C2的公共弦的参数方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( )

A. 消耗1升汽油,乙车最多可行驶5千米
B. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C. 甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D. 某城市机动车最高限速80千米/小时. 相同条件下,在该市用丙车比用乙车更省油
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中错误的是( )
A. 先把高二年级的2000名学生编号为1到2000,再从编号为1到50的50名学生中随机抽取1名学生,其编号为![]() ,然后抽取编号为
,然后抽取编号为![]() ,
, ![]() ,
, ![]() 的学生,这样的抽样方法是系统抽样法
的学生,这样的抽样方法是系统抽样法
B. 线性回归直线![]() 一定过样本中心点
一定过样本中心点![]()
C. 若两个随机变量的线性相关性越强,则相关系数![]() 的值越接近于1
的值越接近于1
D. 若一组数据1、![]() 、3的平均数是2,则该组数据的方差是
、3的平均数是2,则该组数据的方差是![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com