
【题目】设函数f(x)=x2﹣ax(a>0,且a≠1),g(x)=f′(x)(其中f′(x)为f(x)的导函数).
(1)当a=e时,求g(x)的极大值点;
(2)讨论f(x)的零点个数.
【答案】
(1)解:a=e时,g(x)=2x﹣ex,g′(x)=2﹣ex,
令g′(x)=0得:2﹣ex=0,解得x=ln2,
∴当x<ln2时,g′(x)>0;当x>ln2时,g′(x)<0,
∴g(x)的极大值点为ln2.
(2)解:(Ⅰ)当a>1时,f′(x)=2x﹣lnaax,
∴当x≤0时,f′(x)<0,∴f(x)在(﹣∞,0)上为减函数,
∵f(﹣1)=1﹣ ![]() >0,f(0)=﹣1<0,
>0,f(0)=﹣1<0,
∴f(x)在(0,+∞)有一个零点;
当x>0时,令f(x)=0得x2=ax,即lna= ![]() ,
,
令h(x)= ![]() ,则h′(x)=
,则h′(x)= ![]() .
.
∴当0<x<e时,h′(x)>0;当x>e时,h′(x)<0,
∴h(x)在(0,e)上单调递增,在(e,+∞)上单调递减,
做出y=h(x)的图象如下图,
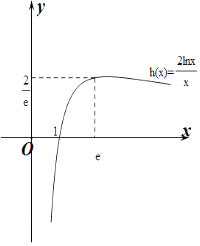
由图象可知:
①当lna> ![]() 即a>e
即a>e ![]() 时,f(x)在(0,+∞)上无零点;
时,f(x)在(0,+∞)上无零点;
②当lna= ![]() 即a=e
即a=e ![]() 时,f(x)在(0,+∞)上有1个零点;
时,f(x)在(0,+∞)上有1个零点;
③当0<lna< ![]() 即1<a<e
即1<a<e ![]() 时,f(x)在(0,+∞)上有2个零点;
时,f(x)在(0,+∞)上有2个零点;
(Ⅱ)当0<a<1时,f′(x)=2x﹣lnaax,
∴当 x>0时,f′(x)>0,∴f(x)在(0,+∞)上是增函数,
∵f(0)=﹣l<0,f(1)=1﹣a>0,
∴f(x)在(0,+∞)上有1个零点;
当x<0时,令f(x)=0得lna= ![]() ,
,
令H(x)= ![]() ,则H′(x)=
,则H′(x)= ![]() ,
,
∴当﹣e<x<0时,H′(x)>0,当x<﹣e时,H′(x)<0,
∴H(x)在(﹣∞,﹣e)上单调递减,在(﹣e,0)上单调递增,
作出y=H(x)的函数图象如图:
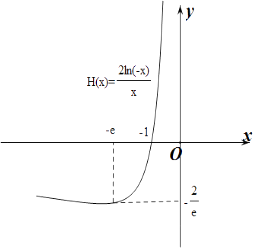
由图象可知:
当lna<﹣ ![]() 即0
即0 ![]() 时,f(x)在(﹣∞,0)上无零点;
时,f(x)在(﹣∞,0)上无零点;
当lna=﹣ ![]() 即a=e
即a=e ![]() 时,f(x)在(﹣∞,0)上有1个零点;
时,f(x)在(﹣∞,0)上有1个零点;
当﹣ ![]() <lna<0即e
<lna<0即e ![]() <a<1时,f(x)在(﹣∞,0)上有2个零点;
<a<1时,f(x)在(﹣∞,0)上有2个零点;
综上:
①当0<a<e ![]() 或a>e
或a>e ![]() 时,f(x)有1个零点;
时,f(x)有1个零点;
②当a=e ![]() 或a=e
或a=e ![]() 时,f(x)有2个零点;
时,f(x)有2个零点;
③当e ![]() <a<1或1<a<e
<a<1或1<a<e ![]() 时,f(x)有3个零点.
时,f(x)有3个零点.
【解析】(1)令g′(x)=0求出g(x)的极值点,判断g′(x)的符号变化即可得出答案;(2)f′(x)=2x﹣lnaax , 对a和x进行讨论,利用零点的存在性定理,结合函数的图象判断零点的个数.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的极值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】某种产品的广告费用支出![]() 与销售额
与销售额![]() 之间有如下的对应数据(单位:万元):
之间有如下的对应数据(单位:万元):
![]()
(1)求![]() 关于
关于![]() 的线性回归直线方程;
的线性回归直线方程;
(2)据此估计广告费用为10万元时销售收入![]() 的值.
的值.
(附:对于线性回归方程![]() ,其中
,其中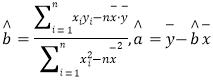 )
)
参考公式: 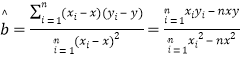
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,其中前三段的频率成等比数列. 
(1)求图中实数a的值;
(2)若该校高一年级共有学生640人,试估计该校高一年级期中考试数学成绩不低于80分的人数;
(3)若从样本中数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取两名学生,记这两名学生成绩在[90,100]内的人数为X,求随机变量X的分布列和期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=e2x , g(x)=kx+1(k∈R). (Ⅰ)若直线y=g(x)和函数y=f(x)的图象相切,求k的值;
(Ⅱ)当k>0时,若存在正实数m,使对任意x∈(0,m),都有|f(x)﹣g(x)|>2x恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线G:y2=2px(p>0),过焦点F的动直线l与抛物线交于A,B两点,线段AB的中点为M.
(Ⅰ)当直线l的倾斜角为 ![]() 时,|AB|=16.求抛物线G的方程;
时,|AB|=16.求抛物线G的方程;
(Ⅱ)对于(Ⅰ)问中的抛物线G,是否存在x轴上一定点N,使得|AB|﹣2|MN|为定值,若存在求出点N的坐标及定值,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1和双曲线C2焦点相同,且离心率互为倒数,F1 , F2是它们的公共焦点,P是椭圆和双曲线在第一象限的交点,若∠F1PF2=60°,则椭圆C1的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com