
【题目】设![]() ,
,![]() ,其中
,其中![]() 是不等于零的常数。
是不等于零的常数。
(1)写出![]() 的定义域;
的定义域;
(2)求![]() 的单调递增区间;
的单调递增区间;
(3)已知函数![]() ,定义:
,定义:![]() ,
,![]() .其中,
.其中,![]() 表示函数
表示函数![]() 在
在![]() 上的最小值,
上的最小值,![]() 表示函数
表示函数![]() 在
在![]() 上的最大值.例如:
上的最大值.例如:![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,当
,当![]() 时,设
时,设![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() ,
,![]() 的取值范围.
的取值范围.
【答案】(1)![]()
(2)![]() 时,
时,![]() 在
在![]() 递增;
递增;![]() 时,
时,![]() 在
在![]() 递增;
递增;![]() 时,
时,![]() 在
在![]() 递增
递增
(3)![]() ,
,![]()
【解析】
(1)考查复合函数的定义域;
(2)![]() 在
在![]() 时在
时在![]() 单调递增,在
单调递增,在![]() 时是对勾函数,
时是对勾函数,![]() 是其极小值点,利用这个求单调递增区间;
是其极小值点,利用这个求单调递增区间;
(3)不等式![]() 恒成立,就是求函数
恒成立,就是求函数![]() 的最大值与最小值,而
的最大值与最小值,而![]() 实际上是对函数
实际上是对函数![]() 与
与![]() 求较小的那个.
求较小的那个.
解:(1)![]() ,
,![]() ,
,![]() 即
即![]() 的定义域为
的定义域为![]() ;
;
(2)设任意的![]() ,
,![]() 且
且![]() ,
,

![]() ,
,![]()
当![]() 时,
时,![]() 在
在![]() 递增;
递增;
当![]() 时,
时,![]() 在
在![]() 递增;
递增;
当![]() 时,
时,![]() 在
在![]() 递增;
递增;
当![]() 时,
时,![]() 在
在![]() 递减,无单调增区间.
递减,无单调增区间.
(3)![]() 的定义域为
的定义域为![]() ,
,![]()
![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
![]() .
.
所以当![]() ,
,![]() 时,
时,![]() ,
,![]() ,在
,在![]() ,
,![]() 单调递减,所以
单调递减,所以![]() ,
,![]() .
.
令![]() ,则
,则![]() 在区间
在区间![]() ,
,![]() 上的最小值为
上的最小值为![]() ,最大值为0.
,最大值为0.
当![]() ,
,![]() 时,
时,![]() ,
,![]() ,在
,在![]() ,
,![]() 单调递增,并且
单调递增,并且![]() (1)
(1)![]()
![]() .当
.当![]() ,
,![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() .
.
![]() .当
.当![]() ,
,![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() ,在
,在![]() ,
,![]() 上单调递减
上单调递减
所以![]() 的最大值为
的最大值为![]()
![]() ,最小值为
,最小值为![]() .
.
综上![]() 的最大值为0,最小值为
的最大值为0,最小值为![]() .
.
![]() ,
,![]() .
.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
【题目】北京时间3月15日下午,谷歌围棋人工智能![]() 与韩国棋手李世石进行最后一轮较量,
与韩国棋手李世石进行最后一轮较量,![]() 获得本场比赛胜利,最终人机大战总比分定格1:4.人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
获得本场比赛胜利,最终人机大战总比分定格1:4.人机大战也引发全民对围棋的关注,某学校社团为调查学生学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图(如图所示),将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.
(Ⅰ)根据已知条件完成列联表,并据此资料你是否有![]() 的把握认为“围棋迷”与性别有关?
的把握认为“围棋迷”与性别有关?

非围棋迷 | 围棋迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
(Ⅱ)将上述调查所得到的频率视为概率,现在从该地区大量学生中,采用随机抽样方法每次抽取1名学生,抽取3次,记被抽取的3名淡定生中的“围棋迷”人数为X。若每次抽取的结果是相互独立的,求X的分布列,期望 E(X) 和方差 D(X) .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“干支纪年法”是中国历法上自古以来使用的纪年方法,甲、乙、丙、丁、戊、己、庚、辛、壬、癸被称为“十天干”,子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥叫做“十二地支”。“天干”以“甲”字开始,“地支”以“子”字开始,两者按干支顺序相配,组成了干支纪年法,其相配顺序为:甲子、乙丑、丙寅…癸酉,甲戌、乙亥、丙子…癸末,甲申、乙酉、丙戌…癸巳,…,共得到![]() 个组成,周而复始,循环记录。2014年是“干支纪年法”中的甲午年,那么2020年是“干支纪年法”中的()
个组成,周而复始,循环记录。2014年是“干支纪年法”中的甲午年,那么2020年是“干支纪年法”中的()
A. 己亥年 B. 戊戌年 C. 庚子年 D. 辛丑年
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() -2
-2![]() +lnx.
+lnx.
(Ⅰ)若a=1,求函数f(x)的极值;
(Ⅱ)若函数f(x)在区间[1,2]上为单调递增函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(Ⅰ)若a=﹣1,证明:函数f(x)是(0,+∞)上的减函数;
(Ⅱ)若曲线y=f(x)在点(1,f(1))处的切线与直线x﹣y=0平行,求a的值;
(Ⅲ)若x>0,证明: ![]() (其中e=2.71828…是自然对数的底数).
(其中e=2.71828…是自然对数的底数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着网络时代的进步,流量成为手机的附带品,人们可以利用手机随时随地的浏览网页,聊天,看视频,因此,社会上产生了很多低头族.某研究人员对该地区18∽50岁的5000名居民在月流量的使用情况上做出调查,所得结果统计如下图所示:
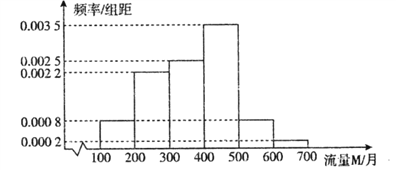
(Ⅰ)以频率估计概率,若在该地区任取3位居民,其中恰有![]() 位居民的月流量的使用情况
位居民的月流量的使用情况
在300M∽400M之间,求![]() 的期望
的期望![]() ;
;
(Ⅱ)求被抽查的居民使用流量的平均值;
(Ⅲ)经过数据分析,在一定的范围内,流量套餐的打折情况![]() 与其日销售份数
与其日销售份数![]() 成线性相关
成线性相关
关系,该研究人员将流量套餐的打折情况![]() 与其日销售份数
与其日销售份数![]() 的结果统计如下表所示:
的结果统计如下表所示:
折扣 | 1折 | 2折 | 3折 | 4折 | 5折 |
销售份数 | 50 | 85 | 115 | 140 | 160 |
试建立![]() 关于
关于![]() 的的回归方程.
的的回归方程.
附注:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
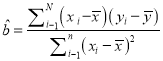 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn,a3=7,S9=27.
(1)求数列{an}的通项公式;
(2)若bn=|an|,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是递增的等差数列,且满足a2a4=21,a1+a5=10.
(1)求{an}的通项公式;
(2)若数列{cn}前n项和Cn=an+1,数列{bn}满足bn=2ncn(n∈N*),求{bn}的前n项和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com