
【题目】如图所示:在五面体ABCDEF中,四边形EDCF是正方形,AD=DE=1,∠ADE=90°,∠ADC=∠DCB=120°.
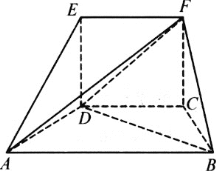
(Ⅰ)求证:平面ABCD⊥平面EDCF;
(Ⅱ)求三棱锥A-BDF的体积.
【答案】(1)见解析:(2)![]()
【解析】
(1)推导出AD⊥DE,CD⊥DE,从而DE⊥平面ABCD,由此能证明平面ABCD⊥平面EDCF,(2)三棱锥A﹣BDF的体积VA﹣BDF=VF﹣ABD![]() ,由此能求出结果.
,由此能求出结果.
(1)证明:∵在五面体ABCDEF中,四边形EDCF是正方形,∠ADE=90°,
∴AD⊥DE,CD⊥DE,
∵AD∩CD=D,∴DE⊥平面ABCD,
∵DE平面EDCF,∴平面ABCD⊥平面EDCF.
(2) 由(1)知DE⊥平面![]() ,所以
,所以![]() 平面
平面![]() . 等腰三角形
. 等腰三角形![]()
又DC∥EF,![]() 平面ABFE,
平面ABFE,![]() 平面ABFE,所以DC∥平面ABFE.
平面ABFE,所以DC∥平面ABFE.
又平面ABCD∩平面ABFE=AB,故AB∥CD.所以四边形![]() 为等腰梯形.又AD=DE,所以AD=CD=CB,由
为等腰梯形.又AD=DE,所以AD=CD=CB,由![]() ,在等腰
,在等腰![]() 中由余弦定理得BD=
中由余弦定理得BD=![]() ,
,![]() AD
AD![]() BD,所以三棱锥
BD,所以三棱锥![]() 的体积为
的体积为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】以下四个命题中真命题的序号是( ).
①平面内到两定点距离之比等于常数![]() 的点的轨迹是圆;
的点的轨迹是圆;
②平面内与定点A(-3,0)和B(3,0)的距离之差等于4的点的轨迹为![]() ;
;
③点P是抛物线![]() 上的动点,点P在x轴上的射影是M,点A的坐标是
上的动点,点P在x轴上的射影是M,点A的坐标是![]() ,则
,则![]() 的最小值是
的最小值是![]() ;
;
④已知P为抛物线![]() 上一个动点,Q为圆
上一个动点,Q为圆![]() 上一个动点,那么点P到点Q的距离与点P到抛物线的准线距离之和的最小值是
上一个动点,那么点P到点Q的距离与点P到抛物线的准线距离之和的最小值是![]()
A.①B.②C.③D.④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将编号为1、2、3、4的四个小球随机的放入编号为1、2、3、4的四个纸箱中,每个纸箱有且只有一个小球,称此为一轮“放球”.设一轮“放球”后编号为![]() 的纸箱放入的小球编号为
的纸箱放入的小球编号为![]() ,定义吻合度误差为
,定义吻合度误差为![]()
![]()
(1) 写出吻合度误差![]() 的可能值集合;
的可能值集合;
(2) 假设![]() 等可能地为1,2,3,4的各种排列,求吻合度误差
等可能地为1,2,3,4的各种排列,求吻合度误差![]() 的分布列;
的分布列;
(3)某人连续进行了四轮“放球”,若都满足![]() ,试按(Ⅱ)中的结果,计算出现这种现象的概率(假定各轮“放球”相互独立);
,试按(Ⅱ)中的结果,计算出现这种现象的概率(假定各轮“放球”相互独立);
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以平面直角坐标系
为参数),以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程及曲线
的直角坐标方程及曲线![]() 上的动点
上的动点![]() 到坐标原点
到坐标原点![]() 的距离
的距离![]() 的最大值;
的最大值;
(Ⅱ)若曲线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,且与
两点,且与![]() 轴相交于点
轴相交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应绿色出行,某市在推出“共享单车”后,又推出“新能源租赁汽车”.每次租车收费的标准由两部分组成:①里程计费:1元/公里;②时间计费:![]() 元/分.已知陈先生的家离上班公司
元/分.已知陈先生的家离上班公司![]() 公里,每天上、下班租用该款汽车各一次.一次路上开车所用的时间记为
公里,每天上、下班租用该款汽车各一次.一次路上开车所用的时间记为![]() (分),现统计了50次路上开车所用时间,在各时间段内频数分布情况如下表所示
(分),现统计了50次路上开车所用时间,在各时间段内频数分布情况如下表所示

将各时间段发生的频率视为概率,一次路上开车所用的时间视为用车时间,范围为![]()
![]() 分.
分.
(1)估计陈先生一次租用新能源租赁汽车所用的时间不低于![]() 分钟的概率;
分钟的概率;
(2)若公司每月发放![]() 元的交通补助费用,请估计是否足够让陈先生一个月上下班租用新能源租赁汽车(每月按
元的交通补助费用,请估计是否足够让陈先生一个月上下班租用新能源租赁汽车(每月按![]() 天计算),并说明理由.(同一时段,用该区间的中点值作代表)
天计算),并说明理由.(同一时段,用该区间的中点值作代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了茎叶图:则下列结论中表述不正确的是
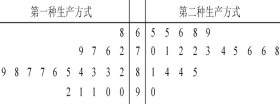
A. 第一种生产方式的工人中,有75%的工人完成生产任务所需要的时间至少80分钟
B. 第二种生产方式比第一种生产方式的效率更高
C. 这40名工人完成任务所需时间的中位数为80
D. 无论哪种生产方式的工人完成生产任务平均所需要的时间都是80分钟.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,曲线C由部分椭圆C1:![]() +
+![]() =1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1与C2的公共点为A,B,其中C1所在椭圆的离心率为
=1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1与C2的公共点为A,B,其中C1所在椭圆的离心率为![]() .
.

(1)求a,b的值;
(2)过点B的直线l与C1,C2分别交于点P,Q(P,Q,A,B中任意两点均不重合),若AP⊥AQ,求直线l
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]()
![]() 的焦距为
的焦距为![]() ,短半轴的长为2,过点P(-2,1)且斜率为1的直线l与椭圆C交于A,B两点.
,短半轴的长为2,过点P(-2,1)且斜率为1的直线l与椭圆C交于A,B两点.
(1)求椭圆C的方程;
(2)求弦AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com