
【题目】某小型水库的管理部门为研究库区水量的变化情况,决定安排两个小组在同一年中各自独立的进行观察研究.其中一个小组研究水源涵养情况.他们通过观察入库的若干小溪和降雨量等因素,随机记录了![]() 天的日入库水量数据(单位:千
天的日入库水量数据(单位:千![]() ),得到下面的柱状图(如图甲).另一小组则研究由于放水、蒸发或渗漏造成的水量消失情况.他们通过观察与水库相连的特殊小池塘的水面下降情况来研究库区水的整体消失量,随机记录了
),得到下面的柱状图(如图甲).另一小组则研究由于放水、蒸发或渗漏造成的水量消失情况.他们通过观察与水库相连的特殊小池塘的水面下降情况来研究库区水的整体消失量,随机记录了![]() 天的库区日消失水量数据(单位:千
天的库区日消失水量数据(单位:千![]() ),并将观测数据整理成频率分布直方图(如图乙).
),并将观测数据整理成频率分布直方图(如图乙).
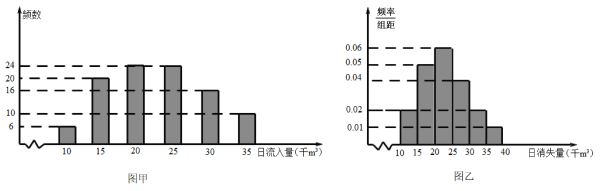
(1)据此估计这一年中日消失水量的平均值;
(2)以频率作为概率,试解决如下问题:
①分别估计日流入水量不少于![]() 千
千![]() 和日消失量不多于
和日消失量不多于![]() 千
千![]() 的概率;
的概率;
②试估计经过一年后,该水库的水量是增加了还是减少了,变化的量是多少?(一年按![]() 天计算),说明理由.
天计算),说明理由.
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 若命题![]() 均为真命题,则命题
均为真命题,则命题![]() 为真命题
为真命题
B. “若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ”
”
C. 在![]() ,“
,“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
D. 命题![]() “
“![]() ”的否定为
”的否定为![]() “
“![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,过左焦点
,过左焦点![]() 且斜率为
且斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() :
:![]() 交椭圆
交椭圆![]() 于
于![]() 两点.
两点.
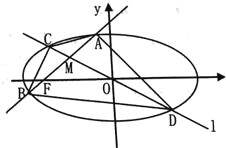
(1)求椭圆![]() 的方程;
的方程;
(2)求证:点![]() 在直线
在直线![]() 上;
上;
(3)是否存在实数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济的发展和个人收入的提高,自2018年10月1日起,个人所得税起征点和税率依法进行调整.调整如下:纳税人的工资、薪金所得,以每月全部收入额减5000元后的余额为应纳税所得额.依照个人所得税税率表,调整前后的计算方法如下表:
个人所得税税率表(调整前) | 个人所得税税率表(调整后) | ||||
免征额3500元 | 免征额5000元 | ||||
级数 | 全月应纳税所得额 | 税率( | 级数 | 全月应纳税所得额 | 税率( |
1 | 不超过1500元的部分 | 3 | 1 | 不超过3000元的部分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 2 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 3 | 超过12000元至25000元的部分 | 20 |
… | … | … | … | … | … |
(1)假如小李某月的工资、薪金等所得税前收入为7500元时,请你帮小李算一下调整后小李的实际收入比调整前增加了多少?
(2)某税务部门在小李所在公司利用分层抽样方法抽取某月100个不同层次员工的税前收入,并制成下面的频数分布表:
收入 (元) |
|
|
|
|
|
|
人数 | 30 | 40 | 10 | 8 | 7 | 5 |
先从收入在![]() 及
及![]() 的人群中按分层抽样抽取7人,再从中选4人作为新纳税法知识宣讲员,用
的人群中按分层抽样抽取7人,再从中选4人作为新纳税法知识宣讲员,用![]() 表示抽到作为宣讲员的收入在
表示抽到作为宣讲员的收入在![]() 元的人数,
元的人数,![]() 表示抽到作为宣讲员的收入在
表示抽到作为宣讲员的收入在![]() 元的人数,随机变量
元的人数,随机变量![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家规定每年的![]() 月
月![]() 日以后的
日以后的![]() 天为当年的暑假.某钢琴培训机构对
天为当年的暑假.某钢琴培训机构对![]() 位钢琴老师暑假一天的授课量进行了统计,如下表所示:
位钢琴老师暑假一天的授课量进行了统计,如下表所示:
授课量(单位:小时) |
|
|
|
|
|
频数 |
|
|
|
|
|
培训机构专业人员统计近![]() 年该校每年暑假
年该校每年暑假![]() 天的课时量情况如下表:
天的课时量情况如下表:
课时量(单位:天) |
|
|
|
|
|
频数 |
|
|
|
|
|
(同组数据以这组数据的中间值作代表)
(1)估计![]() 位钢琴老师一日的授课量的平均数;
位钢琴老师一日的授课量的平均数;
(2)若以(1)中确定的平均数作为上述一天的授课量.已知当地授课价为![]() 元/小时,每天的各类生活成本为
元/小时,每天的各类生活成本为![]() 元/天;若不授课,不计成本,请依据往年的统计数据,估计一位钢琴老师
元/天;若不授课,不计成本,请依据往年的统计数据,估计一位钢琴老师![]() 天暑假授课利润不少于
天暑假授课利润不少于![]() 万元的概率.
万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,
,![]() ,上顶点为
,上顶点为![]() ,右焦点为
,右焦点为![]() ,已知
,已知![]() .
.
(1)证明:![]() .
.
(2)已知直线![]() 的倾斜角为
的倾斜角为![]() ,设
,设![]() 为椭圆
为椭圆![]() 上不同于
上不同于![]() ,
,![]() 的一点,
的一点,![]() 为坐标原点,线段
为坐标原点,线段![]() 的垂直平分线交
的垂直平分线交![]() 于
于![]() 点,过
点,过![]() 且垂直于
且垂直于![]() 的直线交
的直线交![]() 轴于
轴于![]() 点,若
点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知
中,已知![]() 两点分别为椭圆
两点分别为椭圆![]() 的右顶点和上顶点,且
的右顶点和上顶点,且![]() ,右准线
,右准线![]() 的方程为
的方程为![]() .
.

(1)求椭圆的标准方程;
(2)过点![]() 的直线交椭圆于另一点
的直线交椭圆于另一点![]() ,交
,交![]() 于点
于点![]() .若以
.若以![]() 为直径的圆经过原点,求直线
为直径的圆经过原点,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线y=k(x+1)(k>0)与抛物线C![]() 相交于A,B两点,F为C的焦点,若|FA|=2|FB|,则|FA| =( )
相交于A,B两点,F为C的焦点,若|FA|=2|FB|,则|FA| =( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,以坐标原点
为参数,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,取相同长度单位建立极坐标系,曲线
轴的正半轴为极轴,取相同长度单位建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)设射线![]() 与曲线
与曲线![]() 交于不同于极点的点
交于不同于极点的点![]() ,与曲线
,与曲线![]() 交于不同于极点的点
交于不同于极点的点![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com