
【题目】已知f(x)是定义在[﹣1,1]上的奇函数,且f(1)=1,若a,b∈[﹣1,1],a+b≠0时,有 ![]() >0成立.
>0成立.
(Ⅰ)判断f(x)在[﹣1,1]上的单调性,并证明;
(Ⅱ)解不等式:f(2x﹣1)<f(1﹣3x);
(Ⅲ)若f(x)≤m2﹣2am+1对所有的a∈[﹣1,1]恒成立,求实数m的取值范围.
【答案】解:(Ⅰ)任取x1,x2∈[﹣1,1],且x1<x2,则﹣x2∈[﹣1,1],∵f(x)为奇函数,
∴f(x1)﹣f(x2)=f(x1)+f(﹣x2)= ![]() (x1﹣x2),
(x1﹣x2),
由已知得 ![]() >0,x1﹣x2<0,∴f(x1)﹣f(x2)<0,即f(x1)<f(x2).
>0,x1﹣x2<0,∴f(x1)﹣f(x2)<0,即f(x1)<f(x2).
∴f(x)在[﹣1,1]上单调递增.
(Ⅱ)∵f(x)在[﹣1,1]上单调递增,∴ 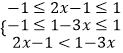
∴不等式的解集为 ![]() .
.
(Ⅲ)∵f(1)=1,f(x)在[﹣1,1]上单调递增.∴在[﹣1,1]上,f(x)≤1.
问题转化为m2﹣2am+1≥1,即m2﹣2am≥0,对a∈[﹣1,1]恒成立.
下面来求m的取值范围.设g(a)=﹣2ma+m2≥0.
①若m=0,则g(a)=0≥0,对a∈[﹣1,1]恒成立.
②若m≠0,则g(a)为a的一次函数,若g(a)≥0,对a∈[﹣1,1]恒成立,
必须g(﹣1)≥0且g(1)≥0,∴m≤﹣2或m≥2.
综上,m=0 或m≤﹣2或m≥2
【解析】1、由题意可得,根据证明函数单调性的定义。任取x1,x2∈[﹣1,1],且x1<x2,判断f(x1)﹣f(x2)的正负即得结果。
2、由题意可得f(x)在[﹣1,1]上单调递增,f(2x﹣1)<f(1﹣3x)可得, 2x-1, 1-3x![]() [﹣1,1], 2x-1>1-3x。求以上不等式的交集。
[﹣1,1], 2x-1>1-3x。求以上不等式的交集。
3、由(2)可知函数f(x)单调递增即有f(x)![]() f(1)=1故f(x)
f(1)=1故f(x)![]() 可表示为
可表示为![]() ,对a∈[﹣1,1]恒成立。令g(a)=﹣2ma+m2 , 若m=0,则g(a)=0对a∈[﹣1,1]恒成立;若m≠0,则g(a)为a的一次函数,根据函数在定义域[﹣1,1]上的最小值大于0,可求得m的取值范围。
,对a∈[﹣1,1]恒成立。令g(a)=﹣2ma+m2 , 若m=0,则g(a)=0对a∈[﹣1,1]恒成立;若m≠0,则g(a)为a的一次函数,根据函数在定义域[﹣1,1]上的最小值大于0,可求得m的取值范围。


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 且a1=1,an+1=2Sn+1,数列{bn}满足a1=b1 , 点P(bn , bn+1)在直线x﹣y+2=0上,n∈N* .
(1)求数列{an},{bn}的通项公式;
(2)设 ![]() ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一名大学生尝试开家小“网店”销售一种学习用品,经测算每售出1盒盖产品获利30元,未售出的商品每盒亏损10元.根据统计资料,得到该商品的月需求量的频率分布直方图(如图所示),该同学为此购进180盒该产品,以x(单位:盒,100≤x≤200)表示一个月内的市场需求量,y(单位:元)表示一个月内经销该产品的利润.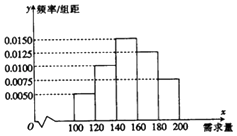
(1)根据直方图估计这个月内市场需求量x的平均数;
(2)将y表示为x的函数;
(3)根据直方图估计这个月利润不少于3800元的概率(用频率近似概率).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cos22x﹣2,给出下列命题:
①β∈R,f(x+β)为奇函数;
②α∈(0, ![]() ),f(x)=f(x+2α)对x∈R恒成立;
),f(x)=f(x+2α)对x∈R恒成立;
③x1 , x2∈R,若|f(x1)﹣f(x2)|=2,则|x1﹣x2|的最小值为 ![]() ;
;
④x1 , x2∈R,若f(x1)=f(x2)=0,则x1﹣x2=kπ(k∈Z).其中的真命题有( )
A.①②
B.③④
C.②③
D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,an+1= ![]() (n∈N*).
(n∈N*).
(1)求证:{ ![]() +
+ ![]() }为等比数列,并求{an}的通项公式an;
}为等比数列,并求{an}的通项公式an;
(2)数列{bn}满足bn=(3n﹣1) ![]() an , 求数列{bn}的前n项和Tn .
an , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为  (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 ![]() (θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为(2
(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为(2 ![]() ,
, ![]() ).
).
(Ⅰ)求直线l以及曲线C的极坐标方程;
(Ⅱ)设直线l与曲线C交于A,B两点,求△PAB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 的定义域为(﹣1,1),满足f(﹣x)=﹣f(x),且f(
的定义域为(﹣1,1),满足f(﹣x)=﹣f(x),且f( ![]() )=
)= ![]() .
.
(1)求函数f(x)的解析式;
(2)证明f(x)在(﹣1,1)上是增函数;
(3)解不等式f(x2﹣1)+f(x)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinx,x∈(0,2π),点P(x,y)是函数f(x)图象上任一点,其中0(0,0),A(2π,0),记△OAP的面积为g(x),则g′(x)的图象可能是( )
A.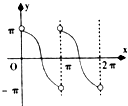
B.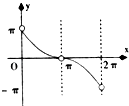
C.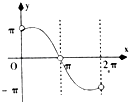
D.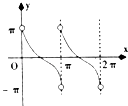
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com