
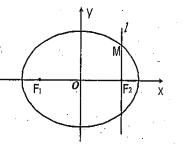
【题目】如图,在直角坐标![]() 中,设椭圆
中,设椭圆![]()
![]() 的左右两个焦点分别为
的左右两个焦点分别为![]() ,过右焦点
,过右焦点![]() 且与
且与![]() 轴垂直的直线
轴垂直的直线![]() 与椭圆
与椭圆![]() 相交,其中一个交点为
相交,其中一个交点为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2>已知![]() 经过点
经过点![]() 且斜率为
且斜率为![]() 直线
直线![]() 与椭圆
与椭圆![]() 有两个不同的
有两个不同的![]() 和
和![]() 交点,请问是否存在常数
交点,请问是否存在常数![]() ,使得向量
,使得向量![]() 与
与![]() 共线?如果存在,求出
共线?如果存在,求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
【答案】(1) ![]() (2)不存在常数
(2)不存在常数![]() ,使得向量
,使得向量![]() 与
与![]() 共线.
共线.
【解析】试题分析:(1)由过右焦点![]() 且与
且与![]() 轴垂直的直线
轴垂直的直线![]() 与椭圆
与椭圆![]() 相交,其中一个交点为
相交,其中一个交点为![]() ,可得
,可得![]() ,再根据椭圆的定义以及勾股定理列方程求得
,再根据椭圆的定义以及勾股定理列方程求得![]() 从而得
从而得![]() ,进而可得椭圆的标准方程;(2)直线
,进而可得椭圆的标准方程;(2)直线![]() 的方程为
的方程为![]() 与椭圆方程联立,可得
与椭圆方程联立,可得![]() ,由
,由![]() ,解得
,解得 ,
, ![]() 与
与![]() 共线等价于
共线等价于![]() ,根据韦达定理以及向量的坐标运算法则可得关于
,根据韦达定理以及向量的坐标运算法则可得关于![]() 的方程,解得
的方程,解得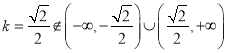 ,从而可得结论.
,从而可得结论.
试题解析:(1)由椭圆定义可知![]() .
.
由题意![]() ,
,![]() .
.
又由![]() △
△![]() 可知
可知 ![]() ,
,![]() ,
,![]() ,
,
又![]() ,得
,得![]() .
.
![]() 椭圆
椭圆![]() 的方程为
的方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,
,
代入椭圆方程,得![]() .
.
整理,得![]() ①
①
因为直线![]() 与椭圆
与椭圆![]() 有两个不同的交点
有两个不同的交点![]() 和
和![]() 等价于
等价于![]() ,
,
解得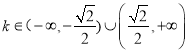 .
.
设![]() ,则
,则![]() =
=![]() ,
,
由①得![]() ②
②
又![]() ③
③
因为![]() , 所以
, 所以![]() .
.
所以![]() 与
与![]() 共线等价于
共线等价于![]() .
.
将②③代入上式,解得![]() .
.
因为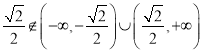
所以不存在常数![]() ,使得向量
,使得向量![]() 与
与![]() 共线.
共线.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知{an}为等差数列,公差为d,且0<d<1,a5≠ ![]() (k∈Z),sin2a3+2sina5cosa5=sin2a7 , 函数f(x)=dsin(wx+4d)(w>0)满足:在
(k∈Z),sin2a3+2sina5cosa5=sin2a7 , 函数f(x)=dsin(wx+4d)(w>0)满足:在 ![]() 上单调且存在
上单调且存在 ![]() ,则w范围是 .
,则w范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.
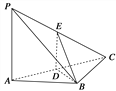
(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共![]() 个,生产一个卫兵需
个,生产一个卫兵需![]() 分钟,生产一个骑兵需
分钟,生产一个骑兵需![]() 分钟,生产一个伞兵需
分钟,生产一个伞兵需![]() 分钟,已知总生产时间不超过
分钟,已知总生产时间不超过![]() 小时,若生产一个卫兵可获利润
小时,若生产一个卫兵可获利润![]() 元,生产一个骑兵可获利润
元,生产一个骑兵可获利润![]() 元,生产一个伞兵可获利润
元,生产一个伞兵可获利润![]() 元.
元.
(1)用每天生产的卫兵个数![]() 与骑兵个数
与骑兵个数![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(2)怎么分配生产任务才能使每天的利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图下图①,等边三角形ABC的边长为2a,CD是AB边上的高,E,F分别是AC和BC边上的点,且满足![]() =k,现将△ABC沿CD翻折成直二面角ADCB,如图下图②.
=k,现将△ABC沿CD翻折成直二面角ADCB,如图下图②.
(1)试判断翻折后直线AB与平面DEF的位置关系,并说明理由;
(2)求二面角BACD的正切值.
① ②
②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点到准线的距离为
的焦点到准线的距离为![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,过这两点分别作抛物线
两点,过这两点分别作抛物线![]() 的切线,且这两条切线相交于点
的切线,且这两条切线相交于点![]() .
.
(1)若![]() 的坐标为
的坐标为![]() ,求
,求![]() 的值;
的值;
(2)设线段![]() 的中点为
的中点为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,过
,过![]() 的直线
的直线![]() 与线段
与线段![]() 为直径的圆相切,切点为
为直径的圆相切,切点为![]() ,且直线
,且直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,证明:
两点,证明: 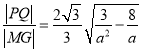 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
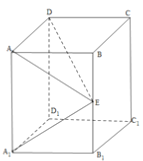
【题目】如图所示,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是矩形,AB=1,BC=![]() ,AA1=2,E是侧棱BB1的中点.
,AA1=2,E是侧棱BB1的中点.
(1)求证:A1E⊥平面AED;
(2)求二面角A﹣A1D﹣E的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com