
【题目】已知椭圆![]() :
:![]() .
.
(1)若抛物线![]() 的焦点与
的焦点与![]() 的焦点重合,求
的焦点重合,求![]() 的标准方程;
的标准方程;
(2)若![]() 的上顶点
的上顶点![]() 、右焦点
、右焦点![]() 及
及![]() 轴上一点
轴上一点![]() 构成直角三角形,求点
构成直角三角形,求点![]() 的坐标;
的坐标;
(3)若![]() 为
为![]() 的中心,
的中心,![]() 为
为![]() 上一点(非
上一点(非![]() 的顶点),过
的顶点),过![]() 的左顶点
的左顶点![]() ,作
,作![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,求证:
,求证:![]() .
.
【答案】(1)抛物线![]() 的标准方程为
的标准方程为![]() 和
和![]() .
.
(2)![]() 或
或![]() .
.
(3)见解析
【解析】
(1)根据椭圆的方程和抛物线的性质即可求出;
(2)按哪个角为直角进行分类,结合数量积为0,计算得到M的坐标.
(3)由B(﹣3,0),BQ∥OP,设直线BQ的方程为x=my﹣3,直线OP的方程为x=my,分别于椭圆的方程联立,求出点Q,N,P的坐标,再根据向量的运算即可证明.
(1) 椭圆![]() 的焦点坐标为
的焦点坐标为![]() 和
和![]() ,抛物线
,抛物线![]() 的标准方程为
的标准方程为![]() 和
和![]() .
.
(2)设点![]() 的坐标为
的坐标为![]() ,
,![]() 的上顶点
的上顶点![]() 的坐标为
的坐标为![]() ,右焦点
,右焦点![]() 的坐标为
的坐标为![]() .
.
当![]() 为直角顶点时,点
为直角顶点时,点![]() 的坐标为
的坐标为![]() ;
;
当![]() 为直角顶点时,
为直角顶点时,![]() ,
,![]() ,由
,由![]() ,解得
,解得![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
因此,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
(3)设直线![]() 的方程为
的方程为![]() (
(![]() ),直线
),直线![]() 的方程为
的方程为![]() .
.
于是点![]() ,
,![]() 的坐标
的坐标![]() ,
,![]() 为方程组
为方程组 的实数解,
的实数解,
解得点![]() 的坐标为
的坐标为![]() .
.
点![]() ,
,![]() 的坐标
的坐标![]() ,
,![]() 为方程组
为方程组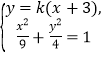 的实数解,解得点
的实数解,解得点![]() 的坐标为
的坐标为![]() .
.
又点![]() 的坐标为
的坐标为![]() .
.
于是![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
即![]() ,得证.
,得证.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】对n个互不相等的正整数,其中任意六个数中都至少存在两个数,使得其中一个能整除另一个.求n的最小值,使得在这n个数中一定存在六个数,其中一个能被另外五个整除.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.

(1)证明:![]() 平面AEC;
平面AEC;
(2)设AP=1,AD=![]() ,三棱锥P-ABD的体积V=
,三棱锥P-ABD的体积V=![]() ,求A到平面PBC的距离.
,求A到平面PBC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有四个小球,分别写有“海”“中”“加”“油”四个字,有放回地从中任取一个小球,取到“加”就停止,用随机模拟的方法估计直到第二次停止的概率:先由计算器产生1到4之间取整数值的随机数,且用1、2、3、4表示取出小球上分别写有“海”“中”“加”“油”四个字,以每两个随机数为一组,代表两次的结果.经随机模拟产生了20组随机数:
13 24 12 32 43 14 24 32 31 21
23 13 32 21 24 42 13 32 21 34
据此估计,直到第二次就停止概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将编号为1,2,…,18的18名乒乓球运动员分配在9张球台上进行单打比赛,规定每一张球台上两选手编号之和均为大于4的平方数.记{7号与18号比赛}为事件p.则p为( ).
A. 不可能事件 B. 概率为![]() 的随机事件
的随机事件
C. 概率为![]() 的随机事件 D. 必然事件
的随机事件 D. 必然事件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间如下:
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |

(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2021年开始,我省将试行“3+1+2“的普通高考新模式,即除语文、数学、外语3门必选科目外,考生再从物理、历史中选1门,从化学、生物、地理、政治中选2门作为选考科目.为了帮助学生合理选科,某中学将高一每个学生的六门科目综合成绩按比例均缩放成5分制,绘制成雷达图.甲同学的成绩雷达图如图所示,下面叙述一定不正确的是( )

A.甲的物理成绩领先年级平均分最多
B.甲有2个科目的成绩低于年级平均分
C.甲的成绩从高到低的前3个科目依次是地理、化学、历史
D.对甲而言,物理、化学、地理是比较理想的一种选科结果
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com