
【题目】已知圆M:(x+1)2+y2=1,圆N:(x-1)2+y2=9,动圆P与圆M外切并与圆N内切,圆心P的轨迹为曲线 C
(Ⅰ)求C的方程;
(Ⅱ)l是与圆P,圆M都相切的一条直线,l与曲线C交于A,B两点,当圆P的半径最长时,求|AB|.
科目:高中数学 来源: 题型:
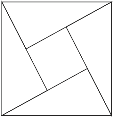
【题目】2002年8月在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,设直角三角形中较小的锐角为![]() ,大正方形的面积是1,小正方形的面积是
,大正方形的面积是1,小正方形的面积是![]() .若
.若![]() ,
,![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,其中
,其中![]() ,若
,若![]() 是
是![]() 的三条边长,则下列结论中正确的是( )
的三条边长,则下列结论中正确的是( )
①存在![]() ,使
,使![]() 、
、![]() 、
、![]() 不能构成一个三角形的三条边
不能构成一个三角形的三条边
②对一切![]() ,都有
,都有![]()
③若![]() 为钝角三角形,则存在
为钝角三角形,则存在![]() ,使
,使![]()
A. ①② B. ①③ C. ②③ D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双十一购物狂欢节,源于淘宝商城(天猫)![]() 年
年![]() 月
月![]() 日举办的网络促销活动,目前已成为中国电子商务行业的年度盛事,某商家为了解“双十一”这一天网购者在其网店一次性购物情况,从这一天交易成功的所有订单里随机抽取了
日举办的网络促销活动,目前已成为中国电子商务行业的年度盛事,某商家为了解“双十一”这一天网购者在其网店一次性购物情况,从这一天交易成功的所有订单里随机抽取了![]() 份,按购物金额(单位:元)进行统计,得到如下频率分布直方图(同一组中的数据用该组区间的中点值做代表计算).
份,按购物金额(单位:元)进行统计,得到如下频率分布直方图(同一组中的数据用该组区间的中点值做代表计算).
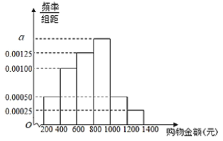
(1)求![]() 的值;
的值;
(2)试估计购物金额的平均数;
(3)若该商家制订了两种不同的促销方案:
方案一:全场商品打八折;
方案二:全场商品优惠如下表:
购物金额范围 |
|
|
|
|
|
|
商家优惠(元) |
|
|
|
|
|
|
如果你是购物者,你认为哪种方案优惠力度更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线![]() (其中
(其中![]() )的焦点
)的焦点![]() 的直线交抛物线于
的直线交抛物线于![]() 两点,且
两点,且![]() 两点的纵坐标之积为
两点的纵坐标之积为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)对于![]() 轴上给定的点
轴上给定的点![]() (其中
(其中![]() ),若过点
),若过点![]() 和
和![]() 两点的直线交抛物线
两点的直线交抛物线![]() 的准线
的准线![]() 点,求证:直线
点,求证:直线![]() 与
与![]() 轴交于一定点.
轴交于一定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,离心率为
,离心率为![]() ,
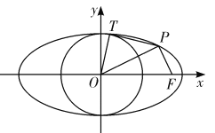
,![]() 是椭圆
是椭圆![]() 上位于第一象限内的任意一点,
上位于第一象限内的任意一点,![]() 为坐标原点,
为坐标原点,![]() 关于
关于![]() 的对称点为
的对称点为![]() ,
,![]() ,圆
,圆![]() :
:![]() .
.
(1)求椭圆![]() 和圆
和圆![]() 的标准方程;
的标准方程;
(2)过点![]() 作
作![]() 与圆
与圆![]() 相切于点
相切于点![]() ,使得点
,使得点![]() ,点
,点![]() 在
在![]() 的两侧.求四边形
的两侧.求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com