Question

【题目】已知函数f（x）=x2﹣4x+1．

（ I）当x∈[0，3]时，画出函数y=f（x）的图象并写出值域；
（II）若函数y=f（x）在区间[a，a+1]上单调，求a的取值范围．

Answer 1

【答案】解：（Ⅰ）当x∈[0，3]时，画出函数y=f（x）=x2﹣4x+1的图象如图：

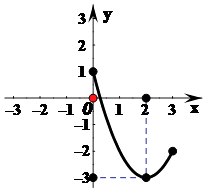
值域为[﹣3，1]．

（Ⅱ）二次函数f（x）=x2﹣4x+1的对称轴为x=2

因为函数y=f（x）在区间[a，a+1]上单调

所以a≥2或a+1≤2

解得a≥2或a≤1

综上，x的取值范围是{a|a≤1，或a≥2}

【解析】（1）根据二次函数的性质，在平面直角坐标系中作出其图象，由图象不难得出值域，（2）由二次函数的解析式可得出其对称轴为x=2，要使得f（x）在给定区间内单调，只需对称轴不在给定区间内，列出不等式即可解得a的取值范围.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识，掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．