Question

【题目】2017年10月1日，为庆祝中华人民共和国成立68周年，来自北京大学和清华大学的6名大学生志愿者被随机平均分配到天安门广场运送矿泉水、打扫卫生、维持秩序这三个岗位服务，且运送矿泉水岗位至少有1名北京大学志愿者的概率是.

(1)求打扫卫生岗位恰好有北京大学、清华大学志愿者各1名的概率；

(2)设随机变量ξ为在维持秩序岗位服务的北京大学志愿者的人数，求ξ的分布列和均值．

Answer 1

【答案】（1）；（2）见解析

【解析】

（1）先根据条件求北京大学志愿者人数，再根据古典概型概率公式求结果，（2）先确定随机变量取法，再求对应概率，列表得分布列，最后根据数学期望公式求期望.

(1)记“至少有1名北京大学志愿者被分到运送矿泉水岗位”为事件A，则事件A的对立事件为“没有北京大学志愿者被分到运送矿泉水岗位”，设有北京大学志愿者x名，1≤x<6，那么P(A)＝1－＝，解得x＝2，即来自北京大学的志愿者有2名，来自清华大学的志愿者有4名．

记“打扫卫生岗位恰好有北京大学、清华大学志愿者各1名”为事件B，则P(B)＝＝，

所以打扫卫生岗位恰好有北京大学、清华大学志愿者各1名的概率是.

(2)在维持秩序岗位服务的北京大学志愿者的人数ξ服从超几何分布，其中N＝6，M＝2，n＝2，于是

P(ξ＝k)＝，k＝0,1,2，

∴P(ξ＝0)＝＝，

P(ξ＝1)＝＝，

P(ξ＝2)＝＝.

所以ξ的分布列为

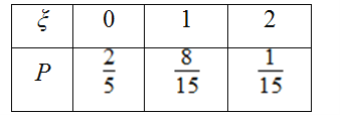
E(ξ)=2/3