
【题目】为了解春季昼夜温差大小与某种子发芽数之间的关系,现在从4月份的30天中随机挑选了5天进行研究,且分别记录了明天昼夜温差与每天100颗种子浸泡后的发芽数,得到如下表格:
日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
温差x/℃ | 10 | 11 | 13 | 12 | 8 |
发芽数y/颗 | 23 | 25 | 30 | 26 | 16 |
从这5天中任选2天,记发芽的种子数分别为![]() ,求事件“
,求事件“![]() 君不小于25”的概率;
君不小于25”的概率;
(2)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5填中的另三天的数据,求出![]() 关于
关于![]() 的线性回归方程,
的线性回归方程,![]() .
.
(参考公式: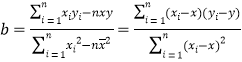 ,
,![]() ).
).
科目:高中数学 来源: 题型:
【题目】若函数![]() 对定义域中任意x均满足
对定义域中任意x均满足![]() ,则称函数
,则称函数![]() 的图象关于点
的图象关于点![]() 对称.
对称.
(1)已知函数![]() 的图象关于点
的图象关于点![]() 对称,求实数m的值;
对称,求实数m的值;
(2)已知函数![]() 在
在![]() 上的图象关于点
上的图象关于点![]() 对称,且当
对称,且当![]() 时,
时,![]() ,求函数
,求函数![]() 在
在![]() 上的解析式;
上的解析式;
(3)在(1)(2)的条件下,当![]() 时,若对任意实数
时,若对任意实数![]() ,恒有
,恒有![]() 成立,求实数a的取值范围.
成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 和点
和点![]() .
.
(1)求椭圆C的焦点坐标和离心率;
(2)设直线l:![]() 与椭圆C交于A,B两点,求弦长
与椭圆C交于A,B两点,求弦长![]() ;
;
(3)求通过M点且被这点平分的弦所在的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax﹣cosx,a≠0.
(1)若函数f(x)为单调函数,求a的取值范围;
(2)若x∈[0,2π],求:当a≥![]() 时,函数f(x)仅有一个零点.
时,函数f(x)仅有一个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中,
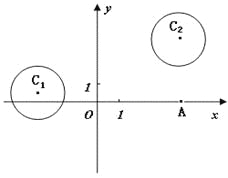
已知圆![]() 和圆
和圆![]() .
.
(1)若直线![]() 过点
过点![]() ,且被圆
,且被圆![]() 截得的弦长为
截得的弦长为![]() ,
,
求直线![]() 的方程;(2)设P为平面上的点,满足:
的方程;(2)设P为平面上的点,满足:
存在过点P的无穷多对互相垂直的直线![]() 和
和![]() ,
,
它们分别与圆![]() 和圆
和圆![]() 相交,且直线
相交,且直线![]() 被圆
被圆![]()
截得的弦长与直线![]() 被圆
被圆![]() 截得的弦长相等,试求所有满足条件的点P的坐标。
截得的弦长相等,试求所有满足条件的点P的坐标。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解青少年的肥胖是否与常喝碳酸饮料有关,现对30名青少年进行调查,得到如下列联表:
常喝 | 不常喝 | 总计 | |
肥胖 | 2 | ||
不肥胖 | 18 | ||
总计 | 30 |
已知从这30名青少年中随机抽取1名,抽到肥胖青少年的概率为![]() .
.
(1)请将列联表补充完整;(2)是否有99.5%的把握认为青少年的肥胖与常喝碳酸饮料有关?
独立性检验临界值表:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com