
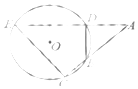
 如图,圆O的弦ED,CB的延长线交于点A.若BD⊥AE,AB=4,BC=2,AD=3,则DE= ;CE= .( )
如图,圆O的弦ED,CB的延长线交于点A.若BD⊥AE,AB=4,BC=2,AD=3,则DE= ;CE= .( )| A. | 5、2$\sqrt{7}$ | B. | 5、7$\sqrt{7}$ | C. | 7 7$\sqrt{2}$ | D. | 5、$\sqrt{7}$ |
科目:高中数学 来源:2015-2016学年江西省南昌市高二文下学期期末考试数学试卷(解析版) 题型:选择题
下列命题的说法错误的是( )
A.命题“若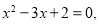 则
则 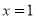 ”的逆否命题为:“若
”的逆否命题为:“若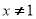 , 则
, 则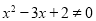 ”.
”.
B.“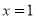 ”是“
”是“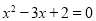 ”的充分不必要条件.
”的充分不必要条件.
C.对于命题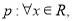
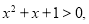 则
则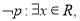
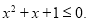
D.若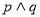 为假命题,则
为假命题,则 均为假命题.
均为假命题.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
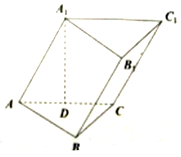 如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1是边长为4的菱形,BC⊥平面ACC1A1,CB=2,点A1在底面ABC上的射影D为棱AC的中点,点A在平面A1CB内的射影为E.
如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1是边长为4的菱形,BC⊥平面ACC1A1,CB=2,点A1在底面ABC上的射影D为棱AC的中点,点A在平面A1CB内的射影为E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
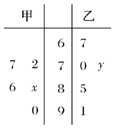 某机械厂今年进行了五次技能考核,其中甲、乙两名技术骨干得分的平均分相等,成绩统计情况如茎叶图所示(其中a是0~9的某个整数);
某机械厂今年进行了五次技能考核,其中甲、乙两名技术骨干得分的平均分相等,成绩统计情况如茎叶图所示(其中a是0~9的某个整数);查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com