
【题目】已知函数![]() ,
, ![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,令函数
时,令函数![]() ,若函数
,若函数![]() 在区间
在区间![]() 上有两个零点,求实数
上有两个零点,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
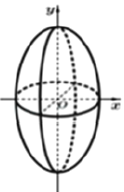
【题目】祖暅是我国齐梁时代的数学家,是祖冲之的儿子,他提出了一条原理:“幂势既同,则积不容易.”这里的“幂”指水平截面的面积.“势”指高,这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体体积相等。于是可把半径相等的半球(底面在下)和圆柱(圆柱高等于半径)放在同一水平面上,圆柱里再放一个半径和高都与圆柱相等的圆锥(锥尖朝下),考察圆柱里被圆锥截剩的立体,这样在同一高度用平行平面截得的半球截面和圆柱中剩余立体截得的截面面积相等,因此半球的体积等于圆柱中剩余立体的体积.设由椭圆![]() 所围成的平面图形绕
所围成的平面图形绕![]() 轴旋转一周后,得一橄榄状的几何体(如图,称为“椭球体”),请类比以上所介绍的应用祖暅原理求球体体积的做法求这个椭球体的体积.其体积等于________.
轴旋转一周后,得一橄榄状的几何体(如图,称为“椭球体”),请类比以上所介绍的应用祖暅原理求球体体积的做法求这个椭球体的体积.其体积等于________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解甲、乙两种产品的质量,从中分别随机抽取了10件样品,测量产品中某种元素的含量(单位:毫克),如图所示是测量数据的茎叶图.规定:当产品中的此中元素的含量不小于18毫克时,该产品为优等品.

(1)试用样品数据估计甲、乙两种产品的优等品率;
(2)若从甲、乙两种产品的优等品中各随机抽取1件,抽到的2件优等品中,“甲产品的含量28毫克优等品必须在内,且乙产品的含量28毫克优等品不包含在内”为事件![]() ,求事件
,求事件![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某二手车交易市场对某型号二手汽车的使用年数![]() 与销售价格
与销售价格![]() (单位:万元/辆)进行整理,得到如下的对应数据:
(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
售价 | 16 | 13 | 9.5 | 7 | 4.5 |
(1)试求![]() 关于
关于![]() 的回归直线方程;(参考公式:
的回归直线方程;(参考公式: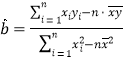 ,
,![]() .)
.)
(2)已知每辆该型号汽车的收购价格为![]() 万元,根据(1)中所求的回归方程,预测
万元,根据(1)中所求的回归方程,预测![]() 为何值时,销售一辆该型号汽车所获得的利润
为何值时,销售一辆该型号汽车所获得的利润![]() 最大?
最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的方程是
的方程是![]() ,曲线
,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求直线![]() 与曲线
与曲线![]() 的极坐标方程;
的极坐标方程;
(2)若射线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直角坐标系中动点![]() ,参数
,参数![]() ,在以原点为极点、
,在以原点为极点、![]() 轴正半轴为极轴所建立的极坐标系中,动点
轴正半轴为极轴所建立的极坐标系中,动点![]() 在曲线
在曲线![]() :
:![]() 上.
上.
(1)求点![]() 的轨迹
的轨迹![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若动点![]() 的轨迹
的轨迹![]() 和曲线
和曲线![]() 有两个公共点,求实数
有两个公共点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅原理也就是“等积原理”,它是由我国南北朝杰出的数学家祖冲之的儿子祖暅首先提出来的,祖暅原理的内容是:夹在两个平行平面间的两个几何体,被平行于这两个平行平面的平面所截,如果截得两个截面的面积总相等,那么这两个几何体的体积相等.已知,两个平行平面间有三个几何体,分别是三棱锥、四棱锥、圆锥(高度都为![]() ),其中:三棱锥的底面是正三角形(边长为
),其中:三棱锥的底面是正三角形(边长为![]() ),四棱锥的底面是有一个角为
),四棱锥的底面是有一个角为![]() 的菱形(边长为
的菱形(边长为![]() ),圆锥的体积为
),圆锥的体积为![]() ,现用平行于这两个平行平面的平面去截三个几何体,如果截得的三个截面的面积相等,那么,下列关系式正确的是( )
,现用平行于这两个平行平面的平面去截三个几何体,如果截得的三个截面的面积相等,那么,下列关系式正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以
),以![]() 为极点,
为极点,![]() 轴非负半轴为极轴建立极坐标系,曲线
轴非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求已知曲线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com