
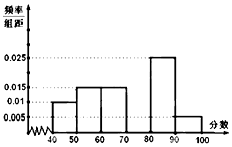
 某校从参加高二年级数学竞赛考试的学生中抽出60名学生,将其成绩分成六段,然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高二年级数学竞赛考试的学生中抽出60名学生,将其成绩分成六段,然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题:分析 (1)第四小组分数在[70,80)内的频率为,即可求出第四个小矩形的高,
(2)同一组数据常用该组区间的中点值作为代表,将中点值与每一组的频率相差再求出它们的和即可求出本次考试的平均分
解答 解:(1)第四小组分数在[70,80)内的频率为:
1-(0.005+0.01+0.015+0.015+0.025)×10=0.30 则第四个小矩形的高为=0.03,
(2)由题意60分以上的各组频率和为:(0.015+0.03+0.025+0.005)×10=0.75,
故这次考试的及格率约为75%,
由45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71,
得本次考试中的平均分约为71:
点评 本题主要考查了频率及频率分布直方图,以及平均数的有关问题,考查运用统计知识解决简单实际问题的能力,数据处理能力和运用意识.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
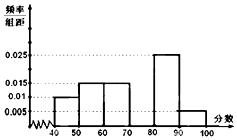 某校从参加高二年级数学竞赛考试的学生中抽出60名学生,将其成绩(均为整数,满分100分)分成六段,然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高二年级数学竞赛考试的学生中抽出60名学生,将其成绩(均为整数,满分100分)分成六段,然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 截两坐标轴所得弦的长度相等 | B. | 与两坐标轴都相切 | ||
| C. | 与两坐标轴相离 | D. | 上述情况都有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
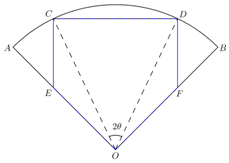 现有半径为R、圆心角(∠AOB)为90°的扇形材料,要裁剪出一个五边形工件OECDF,如图所示.其中E,F分别在OA,OB上,C,D在$\widehat{AB}$上,且OE=OF,EC=FD,∠ECD=∠CDF=90°.记∠COD=2θ,五边形OECDF的面积为S.
现有半径为R、圆心角(∠AOB)为90°的扇形材料,要裁剪出一个五边形工件OECDF,如图所示.其中E,F分别在OA,OB上,C,D在$\widehat{AB}$上,且OE=OF,EC=FD,∠ECD=∠CDF=90°.记∠COD=2θ,五边形OECDF的面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 使用年数 | 2 | 4 | 6 | 8 | 10 |
| 售价 | 16 | 13 | 9.5 | 7 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{2}{3}$) | B. | [$\frac{1}{3}$,$\frac{2}{3}$) | C. | ($\frac{1}{2}$,+∞) | D. | [$\frac{1}{2}$,$\frac{2}{3}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com