
【题目】设 ![]() ,若0≤a≤1,n∈N+且n≥2,求证:f(2x)≥2f(x).
,若0≤a≤1,n∈N+且n≥2,求证:f(2x)≥2f(x).
【答案】证明:∵ ![]() ,
,
∴要证f(2x)≥2f(x),
只要证![]() ,
,
即证![]() (*)
(*)
也即证n[12x+22x+…+(n-1)2x+a·n2x]
≥[1x+2x+…+(n-1)x+a·nx]2 ,
∵0≤a≤1,∴a>a2 , 根据柯西不等式得
n[12x+22x+…+(n-1)2x+a·n2x]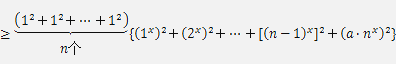 ,
,
≥[1x+2x+…+(n-1)x+a·nx]2 ,
即(*)式显然成立,故原不等式成立.
【解析】本题主要考查了一般形式的柯西不等式,解决问题的关键是将f(2x)>2f(x)具体化,然后再根据式子的结构特点选择合适的证明方法.
【考点精析】本题主要考查了一般形式的柯西不等式的相关知识点,需要掌握一般形式的柯西不等式:![]()
![]() 才能正确解答此题.
才能正确解答此题.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:
【题目】如图,直四棱柱ABCD﹣A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD= ![]() ,AA1=3,E为CD上一点,DE=1,EC=3
,AA1=3,E为CD上一点,DE=1,EC=3 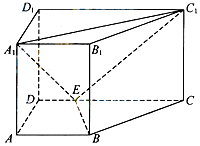
(1)证明:BE⊥平面BB1C1C;
(2)求三棱锥B1﹣EA1C1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对100名六年级学生进行了问卷调查得到如图联表.且平均每天喝500ml以上为常喝,体重超过50kg为肥胖.已知在全部100人中随机抽取1人,抽到肥胖的学生的概率为0.8.
常喝 | 不常喝 | 合计 | |
肥胖 | 60 | ||
不肥胖 | 10 | ||
合计 | 100 |
(1)求肥胖学生的人数并将上面的列联表补充完整;
(2)是否有95%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由. 附:参考公式:x2= ![]()
P(x2≥x0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
x0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=sin(2x+ ![]() )图象上的每个点的横坐标缩短为原来的一半,纵坐标不变,再将所得图象向左平移
)图象上的每个点的横坐标缩短为原来的一半,纵坐标不变,再将所得图象向左平移 ![]() 个单位得到函数g(x)的图象.在g(x)图象的所有对称中心中,离原点最近的对称中心为( )
个单位得到函数g(x)的图象.在g(x)图象的所有对称中心中,离原点最近的对称中心为( )
A.(﹣ ![]() ,0)
,0)
B.( ![]() ,0)
,0)
C.(﹣ ![]() ,0)
,0)
D.( ![]() ,0)
,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某路段的一个检测点对200辆汽车的车速进行检测所得结果的频率分布直方图,则下列说法正确的是( )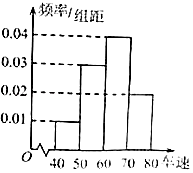
A.平均数为62.5
B.中位数为62.5
C.众数为60和70
D.以上都不对
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 的三个内角 A,B,C 成等差数列,且 a,b,c 分别为角 A,B,C 的对边,求证:(a+b)-1+(b+c)-1=3(a+b+c)-1
的三个内角 A,B,C 成等差数列,且 a,b,c 分别为角 A,B,C 的对边,求证:(a+b)-1+(b+c)-1=3(a+b+c)-1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,则下列三个说法中正确的个数是( )
①存在点E使得直线SA⊥平面SBC
②平面SBC内存在直线与SA平行
③平面ABCE内存在直线与平面SAE平行.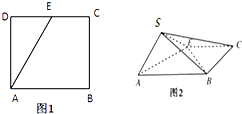
A.0
B.1
C.2
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com