
分析 (1)根据题设条件知S1=a1=1,S2=4a2=$\frac{4}{3}$,S3=9a3=$\frac{3}{2}$,S4=16a4=$\frac{8}{5}$.
(2)猜想Sn=$\frac{2n}{n+1}$,再用数学归纳法对这个猜想加以证明.
解答 解:(1)S1=a1=1
由题意知,S2=4a2=4(S2-S1),
∴S2=$\frac{4}{3}$,
S3=9a3=4(S3-S2),
∴S3=$\frac{3}{2}$
同理得,S4=$\frac{8}{5}$
(2)由(1)S1=1=$\frac{2×1}{1+1}$,S2=$\frac{4}{3}$=$\frac{2×2}{2+1}$,S3=$\frac{3}{2}$=$\frac{3×2}{3+1}$,S4=$\frac{8}{5}$=$\frac{4×2}{4+1}$
猜想{an}的前n项和 Sn=$\frac{2n}{n+1}$,
下面用数学归纳法证明:
①当n=1时,S1=1=$\frac{2×1}{1+1}$,故结论成立,
②假设当n=k时,猜想成立,即Sk=$\frac{2k}{k+1}$,
那么当n=k+1时,Sk+1=Sk+ak=$\frac{2k}{k+1}$+$\frac{{S}_{k+1}}{(k+1)^{2}}$,
∴[1-$\frac{1}{(k+1)^{2}}$]Sk+1=$\frac{2k}{k+1}$,
∴Sk+1=$\frac{2k}{k+1}$•$\frac{(k+1)^{2}}{(k+1)^{2}-1}$=$\frac{2(k+1)}{k+2}$=$\frac{2(k+1)}{(k+1)+1}$
即当n=k+1时,结论也成立
综上①②知,对n∈N*时,Sn=$\frac{2n}{n+1}$,即{an}的前n项和 Sn=$\frac{2n}{n+1}$
点评 本题考查数列的性质和应用,第(1)问要注意递推公式的灵活运用,第二问要注意数学归纳法的证明技巧.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{9}-\frac{y^2}{16}=1$ | B. | $\frac{x^2}{18}-\frac{y^2}{32}=1$ | C. | $\frac{x^2}{9}-\frac{y^2}{25}=1$ | D. | $\frac{x^2}{36}-\frac{y^2}{64}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{2}tan{25°}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{2}$+$\frac{1}{3}$ | C. | $\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$ | D. | $\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
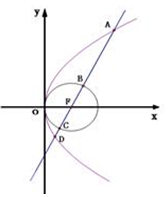 圆F:(x-1)2-y2=1和抛物线y2=4x,过F的直线l与抛物线和圆依次交于A、B、C、D四点
圆F:(x-1)2-y2=1和抛物线y2=4x,过F的直线l与抛物线和圆依次交于A、B、C、D四点查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com