
 型血的人数占总人口数的比为
型血的人数占总人口数的比为 ,现从中随机抽取3人.
,现从中随机抽取3人.  型血的概率;
型血的概率; 型血的人数为
型血的人数为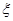 ,求
,求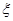 的概率分布与数学期望.
的概率分布与数学期望.科目:高中数学 来源:不详 题型:解答题
| PM2.5日均值m(微克/立方米) | 空气质量等级 |
 | 一级 |
 | 二级 |
 | 超标 |

 表示空气质量达到一级的天数,求
表示空气质量达到一级的天数,求 的分布列;
的分布列;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ξ1 -1 0 1 ξ1 -1 0 1 |
P    |
 ξ2 0 1 2 ξ2 0 1 2 |
P    |
 ξ3 0 1 2 ξ3 0 1 2 |
P    |
 ξ4 1 2 1 ξ4 1 2 1 |
P    |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 寿命/小时 | 100~200 | 200~300 | 300~400 | 400~500 | 500~600 |
| 个数 | 20 | 30 | 80 | 40 | 30 |
| 分组 | 频数 | 频率 |
| 100~200 | ||
| 200~300 | ||
| 300~400 | ||
| 400~500 | ||
| 500~600 | ||
| 合计 |

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 车辆数 | 5 | 10 | 30 | 35 | 15 | 3 | 2 |
| 出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 车辆数 | 14 | 20 | 20 | 16 | 15 | 10 | 5 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 品种甲 | 403 | 397 | 390 | 404 | 388 | 400 | 412 | 406 |
| 品种乙 | 419 | 403 | 412 | 418 | 408 | 423 | 400 | 413 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com