
【题目】如图,三棱柱![]() 中,
中,![]() 底面
底面![]() ,点
,点![]() 是棱
是棱![]() 的中点.
的中点.
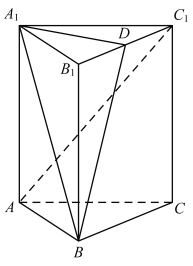
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,
,![]() ,在棱
,在棱![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】2020年1月10日,引发新冠肺炎疫情的COVID-9病毒基因序列公布后,科学家们便开始了病毒疫苗的研究过程.但是类似这种病毒疫苗的研制需要科学的流程,不是一朝一夕能完成的,其中有一步就是做动物试验.已知一个科研团队用小白鼠做接种试验,检测接种疫苗后是否出现抗体.试验设计是:每天接种一次,3天为一个接种周期.已知小白鼠接种后当天出现抗体的概率为![]() ,假设每次接种后当天是否出现抗体与上次接种无关.
,假设每次接种后当天是否出现抗体与上次接种无关.
(1)求一个接种周期内出现抗体次数![]() 的分布列;
的分布列;
(2)已知每天接种一次花费100元,现有以下两种试验方案:
①若在一个接种周期内连续2次出现抗体即终止本周期试验,进行下一接种周期,试验持续三个接种周期,设此种试验方式的花费为![]() 元;
元;
②若在一个接种周期内出现2次或3次抗体,该周期结束后终止试验,已知试验至多持续三个接种周期,设此种试验方式的花费为![]() 元.
元.
比较随机变量![]() 和
和![]() 的数学期望的大小.
的数学期望的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆柱内有一个三棱锥![]() ,
,![]() 为圆柱的一条母线,
为圆柱的一条母线,![]() ,
,![]() 为下底面圆
为下底面圆![]() 的直径,
的直径,![]() .
.
(Ⅰ)在圆柱的上底面圆内是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?证明你的结论.
?证明你的结论.
(Ⅱ)设点![]() 为棱
为棱![]() 的中点,
的中点,![]() ,求四棱锥
,求四棱锥![]() 体积的最大值.
体积的最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从0,1,2,3,4,5,6中取出三个不同的数字组成一个三位数,则这个三位数的各个位上的数字之和为奇数的取法共有_________种.(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年下半年以来,各地区陆续出台了“垃圾分类”的相关管理条例,实行“垃圾分类”能最大限度地减少垃圾处置量,实现垃圾资源利用,改善垃圾资源环境,某部门在某小区年龄处于
年下半年以来,各地区陆续出台了“垃圾分类”的相关管理条例,实行“垃圾分类”能最大限度地减少垃圾处置量,实现垃圾资源利用,改善垃圾资源环境,某部门在某小区年龄处于![]() 岁的人中随机地抽取
岁的人中随机地抽取![]() 人,进行了“垃圾分类”相关知识掌握和实施情况的调查,并把达到“垃圾分类”标准的人称为“环保族”,得到如图示各年龄段人数的频率分布直方图和表中的统计数据.
人,进行了“垃圾分类”相关知识掌握和实施情况的调查,并把达到“垃圾分类”标准的人称为“环保族”,得到如图示各年龄段人数的频率分布直方图和表中的统计数据.
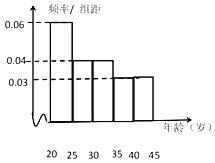
组数 | 分组 | “环保族”人数 | 占本组的频率 |
第一组 |
|
|
|
第二组 |
|
|
|
第三组 |
|
|
|
第四组 |
|
|
|
第五组 |
|
|
|
(1)求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)根据频率分布直方图,估计这![]() 人年龄的平均值(同一组数据用该区间的中点值代替,结果按四舍五入保留整数);
人年龄的平均值(同一组数据用该区间的中点值代替,结果按四舍五入保留整数);
(3)从年龄段在![]() 的“环保族”中采取分层抽样的方法抽取
的“环保族”中采取分层抽样的方法抽取![]() 人进行专访,并在这
人进行专访,并在这![]() 人中选取
人中选取![]() 人作为记录员,求选取的
人作为记录员,求选取的![]() 名记录员中至少有一人年龄在
名记录员中至少有一人年龄在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() .(
.(![]() 为参数)以坐标原点
为参数)以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,点
轴的正半轴为极轴建立极坐标系,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的直角坐标和 l的直角坐标方程;
的直角坐标和 l的直角坐标方程;
(2)把曲线![]() 上各点的横坐标伸长为原来的
上各点的横坐标伸长为原来的![]() 倍,纵坐标伸长为原来的
倍,纵坐标伸长为原来的![]() 倍,得到曲线
倍,得到曲线![]() ,
,![]() 为
为![]() 上动点,求
上动点,求![]() 中点
中点![]() 到直线
到直线![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com