
【题目】德国数学家科拉茨1937年提出了一个著名的猜想:任给一个正整数n,如果n是偶数,就将它减半(即![]() );如果n是奇数,则将它乘3加1(即3n+1),不断重复这样的运算,经过有限步后,一定可以得到1. 对于科拉茨猜想,目前谁也不能证明,也不能否定,现在请你研究:如果对正整数n(首项)按照上述规则施行变换后的第8项为1(注:l可以多次出现),则n的所有不同值的个数为
);如果n是奇数,则将它乘3加1(即3n+1),不断重复这样的运算,经过有限步后,一定可以得到1. 对于科拉茨猜想,目前谁也不能证明,也不能否定,现在请你研究:如果对正整数n(首项)按照上述规则施行变换后的第8项为1(注:l可以多次出现),则n的所有不同值的个数为
A. 4 B. 6 C. 8 D. 32
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
【题目】某工厂生产甲、乙两种产品所得利润分别为![]() 和
和![]() (万元),它们与投入资金
(万元),它们与投入资金![]() (万元)的关系有如下公式:
(万元)的关系有如下公式:![]() ,
,![]() ,今将200万元资金投入生产甲、乙两种产品,并要求对甲、乙两种产品的投入资金都不低于25万元.
,今将200万元资金投入生产甲、乙两种产品,并要求对甲、乙两种产品的投入资金都不低于25万元.
(Ⅰ)设对乙种产品投入资金![]() (万元),求总利润
(万元),求总利润![]() (万元)关于
(万元)关于![]() 的函数关系式及其定义域;
的函数关系式及其定义域;
(Ⅱ)如何分配投入资金,才能使总利润最大,并求出最大总利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中:
①若![]() ,满足
,满足![]() ,则
,则![]() 的最大值为4;
的最大值为4;
②若![]() ,则函数
,则函数![]() 的最小值为3;
的最小值为3;
③若![]() ,满足
,满足![]() ,则
,则![]() 的最大值为
的最大值为![]() ;
;
④若![]() ,满足
,满足![]() ,则
,则![]() 的最小值为2;
的最小值为2;
⑤函数![]() 的最小值为9.
的最小值为9.
正确的有________.(把你认为正确的序号全部写上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知变量![]() 之间的线性回归方程为
之间的线性回归方程为![]() ,且变量
,且变量![]() 之间的一组相关数据如表所示,则下列说法错误的是( )
之间的一组相关数据如表所示,则下列说法错误的是( )
x | 6 | 8 | 10 | 12 |
y | 6 | m | 3 | 2 |
A. 变量![]() 之间呈现负相关关系
之间呈现负相关关系
B. ![]() 的值等于5
的值等于5
C. 变量![]() 之间的相关系数
之间的相关系数![]()
D. 由表格数据知,该回归直线必过点(9,4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着人们生活水平的不断提高,家庭理财越来越引起人们的重视.某一调查机构随机调查了5个家庭的月收入与月理财支出(单位:元)的情况,如下表所示:
月收入 | 8 | 10 | 9 | 7 | 11 |
月理财支出 |
|
|
|
|
|
(I)在下面的坐标系中画出这5组数据的散点图;

(II)根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(III)根据(II)的结果,预测当一个家庭的月收入为![]() 元时,月理财支出大约是多少元?
元时,月理财支出大约是多少元?
(附:回归直线方程![]() 中,
中, ,
,![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥S ABCD中,平面SAD⊥平面ABCD.四边形ABCD为正方形,
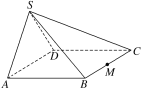
(1)求证:CD⊥平面SAD.
(2)若SA=SD,点M为BC的中点,在棱SC上是否存在点N,使得平面DMN⊥平面ABCD?若存在,请说明其位置,并加以证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax4lnx+bx4﹣c(x>0)在x=1处取得极值﹣3﹣c,其中a,b,c为常数.
(1)试确定a,b的值;
(2)讨论函数f(x)的单调区间;
(3)若对任意x>0,不等式f(x)≥﹣2c2恒成立,求c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系![]() 中,第一象限内有定点
中,第一象限内有定点![]() 和射线
和射线![]() ,已知
,已知![]() ,
,![]() 的倾斜角分别为
的倾斜角分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() 轴上的动点
轴上的动点![]() 与
与![]() ,
,![]() 共线.
共线.
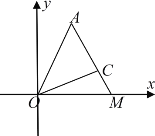
(1)求![]() 点坐标(用
点坐标(用![]() 表示);
表示);
(2)求![]() 面积
面积![]() 关于
关于![]() 的表达式
的表达式![]() ;
;
(3)求![]() 面积的最小时直线
面积的最小时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,下列说法正确的是____________.
,下列说法正确的是____________.
①函数![]() 的定义域为
的定义域为![]() ;
;
②函数![]() 为奇函数;
为奇函数;
③函数![]() 的值域为
的值域为![]() ;
;
④函数在定义域上为增函数;
⑤对于![]() ,均有
,均有![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com