
分析 (1)将k=-5代入可知an=(n-1)(n-4),进而令an<0可得负数项,通过配方可得最小值;
(2)通过an+1>an化简得k>-2n-1,进而可知k>-2-1=-3.
解答 解:(1)若k=-5,则an=n2-5n+4=(n-1)(n-4),
令an<0,则1<n<4,
∴数列中第2、3项共2项为负数,
∵f(x)=x2-5x+4是开口向上,对称轴x=$\frac{5}{2}$的抛物线,
∴当n=2或3时,an有最小值22-5×2+4=-2;
(2)依题意,an+1>an,即(n+1)2+k(n+1)+4>n2+kn+4,
整理得:k>-2n-1,
又∵对于n∈N*,都有an+1>an,
∴k大于-2n-1的最大值,
∴k>-2-1=-3.
点评 本题考查数列的递推式,考查运算求解能力,注意解题方法的积累,属于基础题.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
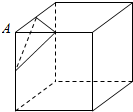 如图,设A是棱长为2的正方体的一个顶点,过从顶点A出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,截去8个三棱锥,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:
如图,设A是棱长为2的正方体的一个顶点,过从顶点A出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,截去8个三棱锥,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
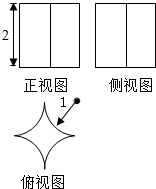 已知某几何体的三视图如图所示,其中俯视图是一个边长为2的正方形切去了四个以顶点为圆心1为半径的四分之一圆,则该几何体的表面积为( )
已知某几何体的三视图如图所示,其中俯视图是一个边长为2的正方形切去了四个以顶点为圆心1为半径的四分之一圆,则该几何体的表面积为( )| A. | 8-π | B. | 8+π | C. | 8-2π | D. | 8+2π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com