
【题目】已知向量 ![]() ,
, ![]() ,
, ![]() .
.
(1)若 ![]() ,且
,且 ![]() ,求
,求 ![]() 的值;
的值;
(2)将函数 ![]() 的图像向右平移
的图像向右平移 ![]() 个单位长度得到函数
个单位长度得到函数 ![]() 的图像,若函数
的图像,若函数 ![]() 在
在 ![]() 上有零点,求
上有零点,求 ![]() 的取值范围.
的取值范围.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】
已知函数![]() ,其中
,其中![]() ,记函数
,记函数![]() 的定义域为
的定义域为![]() .
.
(1)求函数![]() 的定义域
的定义域![]() ;
;
(2)若函数![]() 的最大值为
的最大值为![]() ,求
,求![]() 的值;
的值;
(3)若对于![]() 内的任意实数
内的任意实数![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前n项和为
的前n项和为![]() ,且满足
,且满足![]() +n=2
+n=2![]() (n∈
(n∈![]() )
)
(1)证明:数列![]() 为等比数列,并求数列
为等比数列,并求数列![]() 的通项公式;
的通项公式;
(2)数列![]() 满足
满足![]() (n∈
(n∈![]() ),其前n项和为
),其前n项和为![]() ,试求满足
,试求满足![]() +
+![]() >2018的最小正整数n.
>2018的最小正整数n.
查看答案和解析>>
科目:高中数学 来源: 题型:
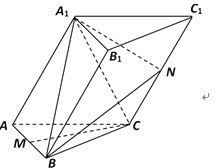
【题目】已知三棱柱![]() 的底面是正三角形,侧面
的底面是正三角形,侧面![]() 为菱形,且
为菱形,且![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 分别是
分别是![]() 的中点.
的中点.
(I)求证:![]() ∥平面
∥平面![]() ;
;
(II)求证:![]() ;
;
(III)求BA1与平面![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·江苏)已知集合X={1,2,3},Yn={1,2,3...,n}(n![]() N*),Sn={(a,b)|a整除b或b整除a, a
N*),Sn={(a,b)|a整除b或b整除a, a![]() X, b
X, b![]() Yn}, 令f(n)表示集合Sn所包含元素的个数。
Yn}, 令f(n)表示集合Sn所包含元素的个数。
(1)写出f(6)的值;
(2)当n≥6时,写出f(n)的表达式,并用数学归纳法证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛两次,记第一次出现的点数为 ![]() ,第二次出现的点数为
,第二次出现的点数为 ![]() ,则事件“
,则事件“ ![]() ”的概率为( )
”的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1= ![]() ,an+1=
,an+1= ![]() (n∈N*).
(n∈N*).
(Ⅰ)求证:数列{ ![]() }是等差数列,并求{an}的通项公式;
}是等差数列,并求{an}的通项公式;
(Ⅱ)设bn+an=l(n∈N*),Sn=b1b2+b2b3+…+bnbn+1 , 试比较an与8Sn的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com