
【题目】11个兴趣班,若干学生参与(可重复参与),每个兴趣班人数相同(招满,人数未知).已知任意九个兴趣班包括了全体学生,而任意八个兴趣班没有包括全体学生求学生总人数的最小值.
科目:高中数学 来源: 题型:
【题目】2022年北京冬奥运动会即第24届冬季奥林匹克运动会将在2022年2月4日至2月20日在北京和张家口举行,某研究机构为了了解大学生对冰壶运动的兴趣,随机从某大学生中抽取了120人进行调查,经统计男生与女生的人数比为11:13,男生中有30人表示对冰壶运动有兴趣,女生中有15人对冰壶运动没有兴趣.
(1)完成![]() 列联表,并判断能否有99%的把握认为“对冰壶运动是否有兴趣与性别有关”?
列联表,并判断能否有99%的把握认为“对冰壶运动是否有兴趣与性别有关”?
有兴趣 | 没有兴趣 | 合计 | |
男 | 30 | ||
女 | 15 | ||
合计 | 120 |
(2)用分层抽样的方法从样本中对冰壶运动有兴趣的学生中抽取8人,求抽取的男生和女生分别为多少人?若从这8人中选取两人作为冰壶运动的宣传员,求选取的2人中恰好有1位男生和1位女生的概率.
附:![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
P | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.076 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在校园篮球赛中,甲、乙两个队10场比赛的得分数据整理成如图所示的茎叶图,下列说法正确的是( )
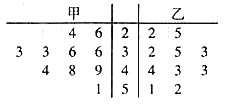
A.乙队得分的中位数是38.5
B.甲、乙两队得分在![]() 分数段频率相等
分数段频率相等
C.乙队的平均得分比甲队的高
D.甲队得分的稳定性比乙队好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ;直线
;直线![]() 的参数方程为
的参数方程为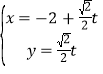 (t为参数).直线
(t为参数).直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某知名电商在![]() 双十一购物狂欢节中成交额再创新高,
双十一购物狂欢节中成交额再创新高,![]() 月
月![]() 日单日成交额达
日单日成交额达![]() 亿元.某店主在此次购物狂欢节期间开展了促销活动,为了解买家对此次促销活动的满意情况,随机抽取了参与活动的
亿元.某店主在此次购物狂欢节期间开展了促销活动,为了解买家对此次促销活动的满意情况,随机抽取了参与活动的![]() 位买家,调查了他们的年龄层次和购物满意情况,得到年龄层次的频率分布直方图和“购物评价为满意”的年龄层次频数分布表.年龄层次的频率分布直方图:
位买家,调查了他们的年龄层次和购物满意情况,得到年龄层次的频率分布直方图和“购物评价为满意”的年龄层次频数分布表.年龄层次的频率分布直方图:
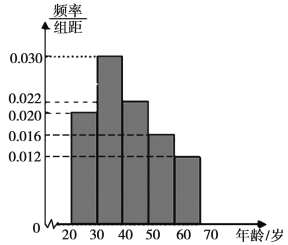
“购物评价为满意”的年龄层次频数分布表:
年龄(岁) |
|
|
|
|
|
频数 |
|
|
|
|
|
(1)估计参与此次活动的买家的平均年龄(同一组中的数据用该组区间的中点值做代表);
(2)若年龄在![]() 岁以下的称为“青年买家”,年龄在
岁以下的称为“青年买家”,年龄在![]() 岁以上(含
岁以上(含![]() 岁)的称为“中年买家”,完成下面的列联表,并判断能否有
岁)的称为“中年买家”,完成下面的列联表,并判断能否有![]() 的把握认为中、青年买家对此次活动的评价有差异?
的把握认为中、青年买家对此次活动的评价有差异?
评价满意 | 评价不满意 | 合计 | |
中年买家 | |||
青年买家 | |||
合计 |
|
附:参考公式: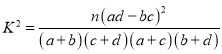 .
.
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列事件是随机事件的是( )
①当x>10时,![]() ; ②当x∈R,x2+x=0有解
; ②当x∈R,x2+x=0有解
③当a∈R关于x的方程x2+a=0在实数集内有解; ④当sinα>sinβ时,α>β( )
A.①②B.②③C.③④D.①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com