
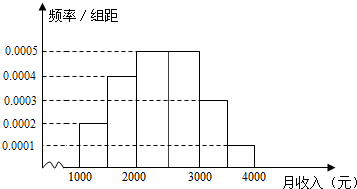
 某市统计局就某地居民的月收入调查了10 000人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1 000,1 500)内).根据频率分布直方图算出样本数据的中位数是( )
某市统计局就某地居民的月收入调查了10 000人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1 000,1 500)内).根据频率分布直方图算出样本数据的中位数是( )| A. | 2360 | B. | 2380 | C. | 2400 | D. | 2420 |
分析 由0.1+0.2=0.3<0.5,0.1+0.2+0.25=0.55>0.5,得中位数在[2000,2500)内,设样本数据的中位数为x,则有0.1+0.2+(x-2000)×0.0005=0.5,由此能求出结果.
解答 解:由频率分布直方图,得月收入在[3000,3500)内的频率为:0.0003×(3500-3000)=0.15,
∵0.0002×(1500-1000)=0.1,
0.0004×(2000-1500)=0.2,
0.0005×(2500-2000)=0.25,
0.1+0.2=0.3<0.5,0.1+0.2+0.25=0.55>0.5,
∴中位数在[2000,2500)内,
设样本数据的中位数为x,
则有0.1+0.2+(x-2000)×0.0005=0.5,
解得x=2400.
故选:C.
点评 本题考查了频率分布直方图和抽样方法及中位数的求解,解题时要认真审题,熟练掌握运用频率分布直方图求中位数的方法,正确理解频率与频数的关系.


科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | $[{1,\frac{1}{2}+ln2}]$ | C. | (-∞,e-1] | D. | [1,e-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
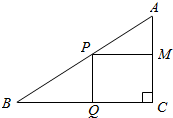 直角三角形ABC的直角顶点为C,且AC=3cm,BC=4cm,P为斜边AB上一点,PQ平行于AC且交BC于点Q,PM平行于BC且交AC于点M,问点P在边AB何处时,矩形PQCM的面积最大?最大面积是多少?
直角三角形ABC的直角顶点为C,且AC=3cm,BC=4cm,P为斜边AB上一点,PQ平行于AC且交BC于点Q,PM平行于BC且交AC于点M,问点P在边AB何处时,矩形PQCM的面积最大?最大面积是多少?查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | $\frac{4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com