
 已知函数f(x)=Asin(ωx+φ)+B(A>0,x∈R,ω>0,|φ|<π)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)+B(A>0,x∈R,ω>0,|φ|<π)的部分图象如图所示.分析 (1)首先,根据图象得到振幅和A,B,ω,从而得到f(x)=2sin(2x+φ)+1,然后,将点(-$\frac{π}{12}$,-1)代入得到φ,即可得解.
(2)化简可得解析式g(x)=2sin(2x-$\frac{π}{3}$)+2,由x∈[0,$\frac{π}{2}$],2x-$\frac{π}{3}$∈[-$\frac{π}{3}$,$\frac{2π}{3}$],根据正弦函数的性质即可得解.
解答 解:(1)根据函数的最大值和最小值得|A|+B=3,B-|A|=-1,
∵A>0,
∴A=2,B=1,
$\frac{1}{2}T$=$\frac{5π}{12}$-(-$\frac{π}{12}$)=$\frac{π}{2}$,
∴T=π,
∴$\frac{2π}{ω}$=π,
∴ω=2,
∴f(x)=2sin(2x+φ)+1,
将点(-$\frac{π}{12}$,-1)代入得到2sin($-\frac{π}{6}$+φ)+1=-1,|φ|<π,
∴φ=-$\frac{π}{3}$,
∴f(x)=2sin(2x-$\frac{π}{3}$)+1.
(2)∵g(x)=f(x+$\frac{π}{6}$)+f(x-$\frac{π}{6}$)=2sin2x+1+2sin(2x-$\frac{2π}{3}$)+1=sin2x-$\sqrt{3}$cos2x+2=2sin(2x-$\frac{π}{3}$)+2,
∵x∈[0,$\frac{π}{2}$],2x-$\frac{π}{3}$∈[-$\frac{π}{3}$,$\frac{2π}{3}$],
∴g(x)=2sin(2x-$\frac{π}{3}$)+2∈[2-$\sqrt{3}$,4].
点评 本题重点考查了由y=Asin(ωx+φ)的部分图象确定其解析式,三角函数的图象与性质及其运用,属于基础题.


 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
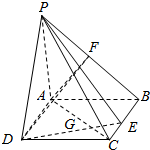 如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,AB=PA=1,AD=$\sqrt{3}$,E、F、G分别是BC、PB、AD上的点,且AF⊥PC,AG=3GD.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,AB=PA=1,AD=$\sqrt{3}$,E、F、G分别是BC、PB、AD上的点,且AF⊥PC,AG=3GD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,⊙O和⊙O′都经过A,B两点,AC是⊙O′的切线,交⊙O于点C,AD是⊙O的切线,交⊙O′于点D,若BC=2,BD=6,则AB的长为2$\sqrt{3}$.
如图,⊙O和⊙O′都经过A,B两点,AC是⊙O′的切线,交⊙O于点C,AD是⊙O的切线,交⊙O′于点D,若BC=2,BD=6,则AB的长为2$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k≤2 | B. | -1<k<0 | C. | -2≤k<-1 | D. | k≤-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com