
【题目】某无缝钢管厂只生产甲、乙两种不同规格的钢管,钢管有内外两个口径,甲种钢管内外两口径的标准长度分别为![]() 和
和![]() ,乙种钢管内外两个口径的标准长度分别为
,乙种钢管内外两个口径的标准长度分别为![]() 和
和![]() .根据长期的生产结果表明,两种规格钢管每根的长度
.根据长期的生产结果表明,两种规格钢管每根的长度![]() 都服从正态分布
都服从正态分布![]() ,长度在
,长度在![]() 之外的钢管为废品,要回炉熔化,不准流入市场,其他长度的钢管为正品.
之外的钢管为废品,要回炉熔化,不准流入市场,其他长度的钢管为正品.
(1)在该钢管厂生产的钢管中随机抽取10根进行检测,求至少有1根为废品的概率;
(2)监管部门规定每种规格钢管的“口径误差”的计算方式为:若钢管的内外两个口径实际长分别为![]() ,标准长分别为
,标准长分别为![]() ,则“口径误差”为
,则“口径误差”为![]() ,按行业生产标准,其中“一级品”“二级品”“合格品”的“口径误差”的范围分别是
,按行业生产标准,其中“一级品”“二级品”“合格品”的“口径误差”的范围分别是![]() (正品钢管中没有“口径误差”大于
(正品钢管中没有“口径误差”大于![]() 的钢管),现分别从甲、乙两种产品的正品中各随机抽取100根,分别进行“口径误差”的检测,统计后,绘制其频率分布直方图如图所示:
的钢管),现分别从甲、乙两种产品的正品中各随机抽取100根,分别进行“口径误差”的检测,统计后,绘制其频率分布直方图如图所示:
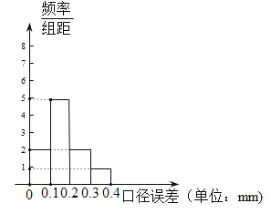

甲种钢管 乙种钢管
已知经销商经销甲种钢管,其中“一级品”的利润率为0.3,“二级品”的利润率为0.18,“合格品”的利润率为0.1;经销乙种钢管,其中“一级品”的利润率为0.25,“二级品”的利润率为0.15,“合格品”的利润率为0.08,若视频率为概率.
(ⅰ)若经销商对甲、乙两种钢管各进了100万元的货,![]() 和
和![]() 分别表示经销甲、乙两种钢管所获得的利润,求
分别表示经销甲、乙两种钢管所获得的利润,求![]() 和
和![]() 的数学期望和方差,并由此分析经销商经销两种钢管的利弊;
的数学期望和方差,并由此分析经销商经销两种钢管的利弊;
(ⅱ)若经销商计划对甲、乙两种钢管总共进100万元的货,则分别在甲、乙两种钢管上进货多少万元时,可使得所获利润的方差和最小?
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() .
.
【答案】(1)![]() ;(2)(ⅰ)
;(2)(ⅰ)![]() ,
,![]() ,
,![]() ,利弊见解析;(ⅱ)甲种钢管上投资25万元,在乙种钢管上投资75万元
,利弊见解析;(ⅱ)甲种钢管上投资25万元,在乙种钢管上投资75万元
【解析】
(1)结合题意,由正态分布的概率进行计算即可;
(2)(ⅰ)根据题意,求解分布列,再根据分布列求解期望和方差即可;
(ⅱ)构造方差和的函数,根据方差的运算性质,利用已知求函数的最小值即可.
(1)由正态分布可知,抽取的1根钢管的长度在![]() 之内的概率为0.9974,
之内的概率为0.9974,
则这10根钢管的长度全在![]() 内的概率为
内的概率为![]() ,
,
则这10根中至少有1根为废品的概率约为![]() .
.
(2)(ⅰ)由利润率和投额可得![]() 可为30万元、18万元、10万元,
可为30万元、18万元、10万元,
![]() 可为25万元、15万元、8万元.
可为25万元、15万元、8万元.
又由直方图可得对应的频率为0.2、0.5、0.3和0.2、0.8、0,
所以随机变量![]() 的分布列为
的分布列为
| 30 | 18 | 10 |
| 0.2 | 0.5 | 0.3 |
![]() (万元),
(万元),
![]() .
.
随机变量![]() 的分布列为
的分布列为
| 25 | 15 | 8 |
| 0.2 | 0.8 | 0 |
![]() (万元),
(万元),![]() .
.
经销商经销甲种钢管的平均利润18万元大于经销乙种钢管的平均利润17万元,
但经销甲种钢管的方差48大于经销乙种钢管的方差16.
所以经销甲种钢管的平均利润大,方差也大,相对不稳定;
而经销乙种钢管的平均利润小,方差也小,相对稳定.
(ⅱ)设经销商进了![]() 万元的甲种钢管,则进了
万元的甲种钢管,则进了![]() 万元的乙种钢管,
万元的乙种钢管,
令![]() 为经销甲种钢管所获利润的方差与经销乙种钢管所获利润的方差的和,则
为经销甲种钢管所获利润的方差与经销乙种钢管所获利润的方差的和,则
![]()
![]()
![]()
![]() .
.
当![]() 时,
时,![]() 的值最小.
的值最小.
故在甲种钢管上投资25万元,在乙种钢管上投资75万元时,
可使经销甲种钢管所获利润的方差与经销乙种钢管所获利润的方差和最小.


科目:高中数学 来源: 题型:
【题目】在某公司举行的年终庆典活动中,主持人利用随机抽奖软件进行抽奖:由电脑随机生成一张如图所示的3![]() 3表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖的总金额为X元.
3表格,其中1格设奖300元,4格各设奖200元,其余4格各设奖100元,点击某一格即显示相应金额.某人在一张表中随机不重复地点击3格,记中奖的总金额为X元.
(1)求概率![]() ;
;
(2)求![]() 的概率分布及数学期望
的概率分布及数学期望![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形,![]() ,侧面
,侧面![]() 为等边三角形且垂直于底面
为等边三角形且垂直于底面![]() ,
,![]() 是
是![]() 的中点.
的中点.
(1)在棱![]() 上取一点
上取一点![]() 使直线
使直线![]() ∥平面
∥平面![]() 并证明;
并证明;
(2)在(1)的条件下,当棱![]() 上存在一点
上存在一点![]() ,使得直线
,使得直线![]() 与底面
与底面![]() 所成角为
所成角为![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
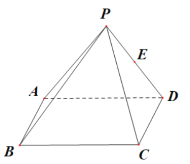
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O:x2+y2=3上的一动点M在x轴上的投影为N,点P满足![]() .
.
(1)求动点P的轨迹C的方程;
(2)若直线l与圆O相切,且交曲线C于点A,B,试求|AB|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某学校高三年级共1000名男生中随机抽取50人测量身高,据测量,被测学生身高全部介于![]() 到
到![]() 之间,将测量结果按如下方式分成八组:第一组
之间,将测量结果按如下方式分成八组:第一组![]() ,第二组
,第二组![]() ,…,第八组
,…,第八组![]() .如图是按上述分组方法得到的频率分布直方图的一部分.其中第六组、第七组、第八组人数依次构成等差数列.
.如图是按上述分组方法得到的频率分布直方图的一部分.其中第六组、第七组、第八组人数依次构成等差数列.
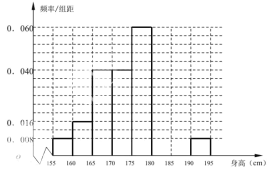
(1)求第六组、第七组的频率,并估计高三年级全体男生身高在![]() 以上(含
以上(含![]() )的人数;
)的人数;
(2)学校决定让这五十人在运动会上组成一个高旗队,在这五十人中要选身高在![]() 以上(含
以上(含![]() )的两人作为队长,求这两人在同一组的概率.
)的两人作为队长,求这两人在同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某景区内有一半圆形花圃,其直径AB为6,O是圆心,且OC⊥AB.在OC上有一座观赏亭Q,其中∠AQC=![]() ,.计划在
,.计划在![]() 上再建一座观赏亭P,记∠POB=θ
上再建一座观赏亭P,记∠POB=θ![]() .
.
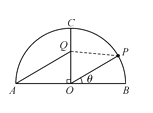
(1)当θ=![]() 时,求∠OPQ的大小;
时,求∠OPQ的大小;
(2)当∠OPQ越大时,游客在观赏亭P处的观赏效果越佳,求游客在观赏亭P处的观赏效果最佳时,角θ的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公园内有一块以![]() 为圆心半径为
为圆心半径为![]() 米的圆形区域.为丰富市民的业余文化生活,现提出如下设计方案:如图,在圆形区域内搭建露天舞台,舞台为扇形
米的圆形区域.为丰富市民的业余文化生活,现提出如下设计方案:如图,在圆形区域内搭建露天舞台,舞台为扇形![]() 区域,其中两个端点
区域,其中两个端点![]() ,
,![]() 分别在圆周上;观众席为梯形
分别在圆周上;观众席为梯形![]() 内切在圆
内切在圆![]() 外的区域,其中
外的区域,其中![]() ,
,![]() ,且
,且![]() ,
,![]() 在点
在点![]() 的同侧.为保证视听效果,要求观众席内每一个观众到舞台
的同侧.为保证视听效果,要求观众席内每一个观众到舞台![]() 处的距离都不超过
处的距离都不超过![]() 米.设
米.设![]() ,
,![]() .问:对于任意
.问:对于任意![]() ,上述设计方案是否均能符合要求?
,上述设计方案是否均能符合要求?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别是角A,B,C的对边,且acosC=(2b﹣c)cosA.
(1)若![]() 3,求△ABC的面积;
3,求△ABC的面积;
(2)若∠B<∠C,求2cos2B+cos2C的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com