解答:解:(1)令t=1-x
2,则y=a
t,
①当a>1时,y=a
t在R上为单调递增函数,而t=1-x
2在(-∞,0]上单调递增,在[0,+∞)上单调递减,
∴
y=a1-x2在(-∞,0]上单调递增,在[0,+∞)上单调递减;
②当0<a<1时,y=a
t在R上为单调递减函数,而t=1-x
2在(-∞,0]上单调递增,在[0,+∞)上单调递减,
∴
y=a1-x2在(-∞,0]上单调递减,在[0,+∞)上单调递增.
综合①②,当a>1时,
y=a1-x2在(-∞,0]上单调递增,在[0,+∞)上单调递减;
当0<a<1时,
y=a1-x2在(-∞,0]上单调递减,在[0,+∞)上单调递增.
(2)∵y=
log(4x-x
3),要使函数有意义,则4x-x
3>0,解得,x<-2或0<x<2,
∴y=
log(4x-x
3)的定义域为(-∞,-2)∪(0,2).
令g(x)=4x-x
3,g′(x)=-3x
2+4,
令g′(x)=-3x
2+4>0,解得,
-<x<,
令g′(x)=-3x
2+4<0,解得,
x<-或x>,
∴g(x)=4x-x
3在
(-,)上单调递增,在
(-∞,-)∪(,+∞)上单调递减,
y=
logx在(0,+∞)上单调递减,结合函数y=
log(4x-x
3)的定义域为(-∞,-2)∪(0,2),
∴函数y=
log(4x-x
3)在
(0,)上单调递减,在(-∞,-2)和
(,2)上单调递增.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 ; (2)y=
; (2)y= tan2x+1;
tan2x+1;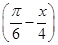 .
.