
【题目】我国2019年新年贺岁大片《流浪地球》自上映以来引发了社会的广泛关注,受到了观众的普遍好评.假设男性观众认为《流浪地球》好看的概率为![]() ,女性观众认为《流浪地球》好看的概率为
,女性观众认为《流浪地球》好看的概率为![]() ,某机构就《流浪地球》是否好看的问题随机采访了4名观众(其中2男2女).
,某机构就《流浪地球》是否好看的问题随机采访了4名观众(其中2男2女).
(1)求这4名观众中女性认为好看的人数比男性认为好看的人数多的概率;
(2)设![]() 表示这4名观众中认为《流浪地球》好看的人数,求
表示这4名观众中认为《流浪地球》好看的人数,求![]() 的分布列与数学期望.
的分布列与数学期望.
【答案】(1)![]() (2)见解析,
(2)见解析,![]()
【解析】
设![]() 表示2名女性观众中认为好看的人数,
表示2名女性观众中认为好看的人数,![]() 表示2名男性观众中认为好看的人数,可得
表示2名男性观众中认为好看的人数,可得![]() ,
,![]() .
.
(1)设事件![]() 表示“这4名观众中女性认为好看的人数比男性认为好看的人数多”,
表示“这4名观众中女性认为好看的人数比男性认为好看的人数多”,
![]() 利用互斥事件与相互独立事件的概率计算公式即可得出.
利用互斥事件与相互独立事件的概率计算公式即可得出.
(2)![]() 的可能取值为0,1,2,3,4,
的可能取值为0,1,2,3,4,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,利用互斥事件与相互独立事件的概率计算公式即可得出概率、分布列及其数学期望.
,利用互斥事件与相互独立事件的概率计算公式即可得出概率、分布列及其数学期望.
解:设![]() 表示2名女性观众中认为好看的人数,
表示2名女性观众中认为好看的人数,![]() 表示2名男性观众中认为好看的人数,
表示2名男性观众中认为好看的人数,
则![]() ,
,![]() .
.
(1)设事件A表示“这4名观众中女性认为好看的人数比男性认为好看的人数多”,则
![]()
![]() .
.
(2)![]() 的可能取值为0,1,2,3,4,
的可能取值为0,1,2,3,4,
![]() ,
,
![]()
![]()
![]()
![]()
![]()
∴![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
所以![]()


科目:高中数学 来源: 题型:
【题目】如图所示的几何体![]() 中,底面
中,底面![]() 为菱形,
为菱形, ![]() ,
, ![]() ,
, ![]() 与
与![]() 相交于
相交于![]() 点,四边形
点,四边形![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 底面
底面![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从抛物线![]() 上各点向x轴作垂线,垂线段中点的轨迹为E.
上各点向x轴作垂线,垂线段中点的轨迹为E.

(1)求曲线E的方程;
(2)若直线![]() 与曲线E相交于A,B两点,求证:
与曲线E相交于A,B两点,求证:![]() ;
;
(3)若点F为曲线E的焦点,过点![]() 的直线与曲线E交于M,N两点,直线
的直线与曲线E交于M,N两点,直线![]() ,
,![]() 分别与曲线E交于C,D两点,设直线
分别与曲线E交于C,D两点,设直线![]() ,
,![]() 斜率分别为
斜率分别为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
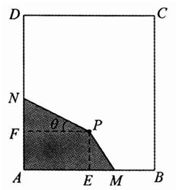
【题目】(题文)如图,长方形材料![]() 中,已知
中,已知![]() ,
,![]() .点
.点![]() 为材料
为材料![]() 内部一点,
内部一点,![]() 于
于![]() ,
,![]() 于
于![]() ,且
,且![]() ,
,![]() . 现要在长方形材料
. 现要在长方形材料![]() 中裁剪出四边形材料
中裁剪出四边形材料![]() ,满足
,满足![]() ,点
,点![]() 、
、![]() 分别在边
分别在边![]() ,
,![]() 上.
上.
(1)设![]() ,试将四边形材料
,试将四边形材料![]() 的面积表示为
的面积表示为![]() 的函数,并指明
的函数,并指明![]() 的取值范围;
的取值范围;
(2)试确定点![]() 在
在![]() 上的位置,使得四边形材料
上的位置,使得四边形材料![]() 的面积
的面积![]() 最小,并求出其最小值.
最小,并求出其最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆:![]() 的离心率为
的离心率为![]() ,y轴于椭圆相交于A、B两点,
,y轴于椭圆相交于A、B两点,![]() ,C、D是椭圆上异于A、B的任意两点,且直线AC、BD相交于点M,直线AD、BC相交于点N.
,C、D是椭圆上异于A、B的任意两点,且直线AC、BD相交于点M,直线AD、BC相交于点N.
![]() 求椭圆的方程;
求椭圆的方程;
![]() 求直线MN的斜率.
求直线MN的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com