
【题目】已知抛物线![]() 和
和![]() 轴上的定点
轴上的定点![]() ,过抛物线焦点作一条直线交
,过抛物线焦点作一条直线交![]() 于
于![]() 、
、![]() 两点,连接
两点,连接![]() 并延长,交
并延长,交![]() 于
于![]() 、
、![]() 两点.
两点.
(1)求证:直线![]() 过定点;
过定点;
(2)求直线![]() 与直线
与直线![]() 最大夹角为
最大夹角为![]() ,求
,求![]() .
.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)当直线![]() 、
、![]() 斜率不存在时,可直接求解;当直线
斜率不存在时,可直接求解;当直线![]() 、
、![]() 斜率存在时,设直线
斜率存在时,设直线![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,不妨设
,不妨设![]() ,联立方程组得
,联立方程组得![]() ,
,![]() ,
,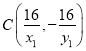 ,
,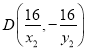 ,结合
,结合![]() 可得直线
可得直线![]() ,即可得证;
,即可得证;
(2)当直线![]() 斜率存在时,易证
斜率存在时,易证![]() ,利用
,利用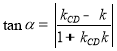 求出最大值即可得解.
求出最大值即可得解.
(1)证明:由题意知抛物线焦点![]() ,
,
当直线![]() 斜率不存在时,直线
斜率不存在时,直线![]() ,易得
,易得![]() ,
,![]() ,
,
则直线![]() ,
,![]() ,
,
所以点![]() ,
,![]() ,此时直线
,此时直线![]() ;
;
当线![]() 斜率存在时,设直线
斜率存在时,设直线![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,不妨设
,不妨设![]() ,
,
则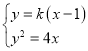 ,化简得
,化简得![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
①当![]() 时,则
时,则![]() ,所以
,所以![]() ,
,![]() ,点
,点![]() ,
,
所以直线![]() ,点
,点![]() ,
,
直线![]() ,则
,则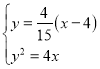 解得点
解得点![]() ,
,
所以直线![]() ;
;
②当![]() 时,此时直线
时,此时直线![]() ,
,
则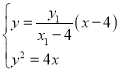 ,结合
,结合![]() 化简得
化简得![]() ,
,
此方程有一根为![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以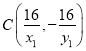 ,
,
同理可得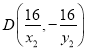 ,
,
由![]() ,
,![]() ,
,![]() 可得
可得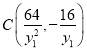 ,
,![]() ,
,
所以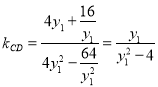 ,
,
所以直线![]() ,化简得
,化简得![]() ,
,
可得直线![]() 过点
过点![]() ;
;
综上,直线![]() 恒过点
恒过点![]() ;
;
(2)由(1)知,当直线![]() 斜率不存在时,
斜率不存在时,![]() ;
;
当直线斜率![]() 存在时,
存在时,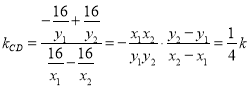 ,
,
设直线![]() 与直线
与直线![]() 的夹角为
的夹角为![]() ,
,
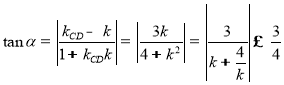 ,当且仅当
,当且仅当![]() 时,等号成立,
时,等号成立,
所以对于直线![]() 与直线
与直线![]() 最大夹角
最大夹角![]() ,
,![]() .
.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 经过定点
经过定点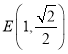 ,其左右集点分别为
,其左右集点分别为![]() ,
,![]() 且
且![]() ,过右焦
,过右焦![]() 且与坐标轴不垂直的直线l与椭圈交于P,Q两点.
且与坐标轴不垂直的直线l与椭圈交于P,Q两点.
(1)求椭圆C的方程:
(2)若O为坐标原点,在线段![]() 上是否存在点
上是否存在点![]() ,使得以
,使得以![]() ,
,![]() 为邻边的平行四边形是菱形?若存在,求出m的取值范围;若不存在,请说明理由.
为邻边的平行四边形是菱形?若存在,求出m的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点![]() 在正视图上的对应点为
在正视图上的对应点为![]() ,圆柱表面上的点
,圆柱表面上的点![]() 在左视图上的对应点为
在左视图上的对应点为![]() ,则在此圆柱侧面上,从
,则在此圆柱侧面上,从![]() 到
到![]() 的路径中,最短路径的长度为( )
的路径中,最短路径的长度为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为进一步规范校园管理,强化饮食安全,提出了“远离外卖,健康饮食”的口号.当然,也需要学校食堂能提供安全丰富的菜品来满足同学们的需求.在学期末,校学生会为了调研学生对本校食堂A部和B部的用餐满意度,从在A部和B部都用过餐的学生中随机抽取了200人,每人分别对其评分,满分为100分.随后整理评分数据,将分数分成6组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,第6组
,第6组![]() ,得到A部分数的频率分布直方图和B部分数的频数分布表.
,得到A部分数的频率分布直方图和B部分数的频数分布表.
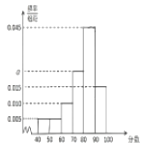
分数区间 | 频数 |
| 7 |
| 18 |
| 21 |
| 24 |
| 70 |
| 60 |
定义:学生对食堂的“满意度指数”
分数 |
|
|
|
|
|
|
满意度指数 | 0 | 1 | 2 | 3 | 4 | 5 |
(1)求A部得分的中位数(精确到小数点后一位);
(2)A部为进一步改善经营,从打分在80分以下的前四组中,采用分层抽样的方法抽取8人进行座谈,再从这8人中随机抽取3人参与“端午节包粽子”实践活动,在第3组抽到1人的情况下,第4组抽到2人的概率;
(3)如果根据调研结果评选学生放心餐厅,应该评选A部还是B部(将频率视为概率)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为F,点
的左焦点为F,点![]() ,过M的直线与椭圆E交于A,B两点,线段AB中点为C,设椭圆E在A,B两点处的切线相交于点P,O为坐标原点.
,过M的直线与椭圆E交于A,B两点,线段AB中点为C,设椭圆E在A,B两点处的切线相交于点P,O为坐标原点.
(1)证明:O、C、P三点共线;
(2)已知![]() 是抛物线
是抛物线![]() 的弦,所在直线过该抛物线的准线与y轴的交点,
的弦,所在直线过该抛物线的准线与y轴的交点,![]() 是弦
是弦![]() 在两端点处的切线的交点,小明同学猜想:
在两端点处的切线的交点,小明同学猜想:![]() 在定直线上.你认为小明猜想合理吗?若合理,请写出
在定直线上.你认为小明猜想合理吗?若合理,请写出![]() 所在直线方程;若不合理,请说明理由.
所在直线方程;若不合理,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C1:x2=2py(p>0),圆C2:x2+y2﹣8y+12=0的圆心M到抛物线C1的准线的距离为![]() ,点P是抛物线C1上一点,过点P,M的直线交抛物线C1于另一点Q,且|PM|=2|MQ|,过点P作圆C2的两条切线,切点为A、B.
,点P是抛物线C1上一点,过点P,M的直线交抛物线C1于另一点Q,且|PM|=2|MQ|,过点P作圆C2的两条切线,切点为A、B.
(Ⅰ)求抛物线C1的方程;
(Ⅱ)求直线PQ的方程及![]()
![]()
![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程:
的参数方程: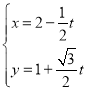 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点,![]() 轴非负半轴为极轴(取相同单位长度)建立极坐标系,圆
轴非负半轴为极轴(取相同单位长度)建立极坐标系,圆![]() 的极坐标方程为:
的极坐标方程为:![]() .
.
(1)将直线![]() 的参数方程化为普通方程,圆
的参数方程化为普通方程,圆![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)求圆![]() 上的点到直线
上的点到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)若![]() ,求曲线
,求曲线![]() 与直线
与直线![]() 的两个交点之间的距离;
的两个交点之间的距离;
(2)若曲线![]() 上的点到直线
上的点到直线![]() 距离的最大值为
距离的最大值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】手机运动计步已成为一种时尚,某中学统计了该校教职工一天行走步数(单位:百步),绘制出如下频率分布直方图:
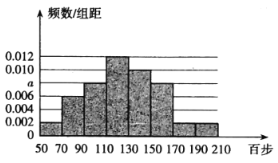
(Ⅰ)求直方图中![]() 的值,并由频率分布直方图估计该校教职工一天步行数的中位数;
的值,并由频率分布直方图估计该校教职工一天步行数的中位数;
(Ⅱ)若该校有教职工175人,试估计一天行走步数不大于130百步的人数;
(Ⅲ)在(Ⅱ)的条件下该校从行走步数大于150百步的3组教职工中用分层抽样的方法选取6人参加远足活动,再从6人中选取2人担任领队,求这两人均来自区间![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com