
【题目】已知函数![]()
(1)求函数![]() 的单调区间;
的单调区间;
(2)设![]() ,若对任意
,若对任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】某港口有一个泊位,现统计了某100艘轮船在该泊位停靠的时间(单位:小时),如果停靠时间不足半小时按半小时计时,超过半小时不足1小时按1小时计时,以此类推,统计结果如下表:

(1)设该月100艘轮船在该泊位的平均停靠时间为![]() 小时,求
小时,求![]() 的值;
的值;
(2)假定某天只有甲、乙两艘轮船需要在该泊位停靠![]() 小时,且在一昼夜的时间段中随机到达,求这两艘轮船至少有一艘在停靠该泊位时必须等待的概率.
小时,且在一昼夜的时间段中随机到达,求这两艘轮船至少有一艘在停靠该泊位时必须等待的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生产企业研发了一种新产品,该新产品在某网店试销一个阶段后得到销售单价![]() 和月销售量
和月销售量![]() 之间的一组数据,如下表所示:
之间的一组数据,如下表所示:
销售单价 | 9 | 9.5 | 10 | 10.5 | 11 |
月销售量 | 11 | 10 | 8 | 6 | 5 |
(Ⅰ)根据统计数据,求出![]() 关于
关于![]() 的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;
的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;
(Ⅱ)生产企业与网店约定:若该新产品的月销售量不低于10万件,则生产企业奖励网店1万元;若月销售量不低于8万件且不足10万件,则生产企业奖励网店5000元;若月销售量低于8万件,则没有奖励.现用样本估计总体,从上述5个销售单价中任选2个销售单价,求抽到的产品含有月销量量不低于10万件的概率.
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为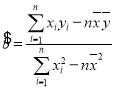 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方![]() 中,
中,![]() ,
,![]() ,E为
,E为![]() 的中点,以
的中点,以![]() 为折痕,把
为折痕,把![]() 折起到
折起到![]() 的位置,且平面
的位置,且平面![]() 平面
平面![]() .
.

(1)求证:![]() ;
;
(2)在棱![]() 上是否存在一点P,使得
上是否存在一点P,使得![]() 平面
平面![]() ,若存在,求出点P的位置,若不存在,请说明理由.
,若存在,求出点P的位置,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产![]() ,
,![]() ,
,![]() 三种纪念品,每种纪念品均有普通型和精品型两种,某一天产量如下表(单位:个):
三种纪念品,每种纪念品均有普通型和精品型两种,某一天产量如下表(单位:个):
普通型 | 精品型 | |
纪念品 | 800 | 200 |
纪念品 |
| 150 |
纪念品 | 500 | 350 |
现采用分层抽样的方法在这一天生产的纪念品中抽取100个,其中有![]() 种纪念品40个.
种纪念品40个.
(1)若再用分层抽样的方法在所有![]() 种纪念品中抽取一个容量为13的样本.将该样本看成一个总体,从中任取2个纪念品,求至少有1个精品型纪念品的概率(用最简分数表示);
种纪念品中抽取一个容量为13的样本.将该样本看成一个总体,从中任取2个纪念品,求至少有1个精品型纪念品的概率(用最简分数表示);
(2)从![]() 种精品型纪念品中抽取6个,其某种指标的数据分别如下:4,7,
种精品型纪念品中抽取6个,其某种指标的数据分别如下:4,7,![]() ,
,![]() ,8,5.把这6个数据看作一个总体,其均值为7、方差为6,求
,8,5.把这6个数据看作一个总体,其均值为7、方差为6,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列事件A,B是独立事件的是( )
A. 一枚硬币掷两次,A=“第一次为正面向上”,B=“第二次为反面向上”
B. 袋中有两个白球和两个黑球,不放回地摸两球,A=“第一次摸到白球”,B=“第二次摸到白球”
C. 掷一枚骰子,A=“出现点数为奇数”,B=“出现点数为偶数”
D. A=“人能活到20岁”,B=“人能活到50岁”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某冷饮店的经营状况,随机记录了该店![]() 月的月营业额
月的月营业额![]() (单位:万元)与月份
(单位:万元)与月份![]() 的数据,如下表:
的数据,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 关于
关于![]() 的回归直线方程
的回归直线方程![]() ;
;
(2)若在这样本点中任取两点,求恰有一点在回归直线上的概率.
附:回归直线方程![]() 中,
中,

 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com