
【题目】如图,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC的中心为O。D、E、F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形。沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱锥。当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为_______。

科目:高中数学 来源: 题型:
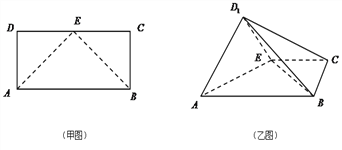
【题目】【2017四川宜宾二诊】如甲图所示,在矩形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起到
折起到![]() 位置,使平面
位置,使平面![]() 平面
平面![]() ,得到乙图所示的四棱锥
,得到乙图所示的四棱锥![]() .
.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(x1 , y1),B(x2 , y2)是函数f(x)= 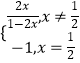 的图象上的任意两点(可以重合),点M在直线x=
的图象上的任意两点(可以重合),点M在直线x= ![]() 上,且
上,且 ![]() =
= ![]() .
.
(1)求x1+x2的值及y1+y2的值;
(2)已知S1=0,当n≥2时,Sn=f( ![]() )+f(
)+f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() ),求Sn .
),求Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把函数f(x)=sin(2x+φ)(|φ|< ![]() )的图象上的所有点向左平移
)的图象上的所有点向左平移 ![]() 个单位长度,得到函数y=g(x)的图象,且g(﹣x)=g(x),则( )
个单位长度,得到函数y=g(x)的图象,且g(﹣x)=g(x),则( )
A.y=g(x)在(0, ![]() )单调递增,其图象关于直线x=
)单调递增,其图象关于直线x= ![]() 对称
对称
B.y=g(x)在(0, ![]() )单调递增,其图象关于直线x=
)单调递增,其图象关于直线x= ![]() 对称
对称
C.y=g(x)在(0, ![]() )单调递减,其图象关于直线x=
)单调递减,其图象关于直线x= ![]() 对称
对称
D.y=g(x)在(0, ![]() )单调递减,其图象关于直线x=
)单调递减,其图象关于直线x= ![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(4,3),
=(4,3), ![]() =(2,﹣1),O为坐标原点,P是直线AB上一点.
=(2,﹣1),O为坐标原点,P是直线AB上一点.
(1)若点P是线段AB的中点,求向量 ![]() 与向量
与向量 ![]() 夹角θ的余弦值;
夹角θ的余弦值;
(2)若点P在线段AB的延长线上,且| ![]() |=
|= ![]() |
| ![]() |,求点P的坐标.
|,求点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知在四棱锥P﹣ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,PA= ![]() ,AB=1.AD=2.∠BAD=120°,E,F,G,H分别是BC,PB,PC,AD的中点.
,AB=1.AD=2.∠BAD=120°,E,F,G,H分别是BC,PB,PC,AD的中点.
(Ⅰ)求证:PH∥平面GED;
(Ⅱ)过点F作平面α,使ED∥平面α,当平面α⊥平面EDG时,设PA与平面α交于点Q,求PQ的长.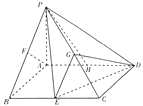
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg), 其频率分布直方图如下:

(1)记A表示事件“旧养殖法的箱产量低于50 kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50 kg | 箱产量≥50 kg | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,对这两种养殖方法的优劣进行比较.
附:
P( | 0.050 0.010 0.001 |
k | 3.841 6.635 10.828 |
![]() .
. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com