
(本题满分12分)
设 ,且
,且 满足
满足
(1)求 的值.
的值.
(2)求 的值.
的值.
科目:高中数学 来源: 题型:解答题
已知函数f(x)=2sinxcosx+cos2x(x∈R).
(1)求f(x)的最小正周期和最大值;
(2)若θ为锐角,且f(θ+ )=
)=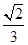 ,求tan2θ的值.
,求tan2θ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)已知函数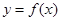
 .
.
(1)求函数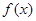 的最小正周期和最大值;
的最小正周期和最大值;
(2)在给出的直角坐标系中,画出函数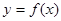 在区间
在区间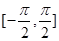 上的图象.
上的图象.
(3)设0<x<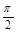 ,且方程
,且方程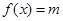 有两个不同的实数根,求实数m的取值范围.
有两个不同的实数根,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分)如图,有一块边长为1(百米)的正方形区域ABCD,在点A处有一个可转动的探照灯,其照射角 始终为
始终为 (其中点P,Q分别在边BC,CD上),设
(其中点P,Q分别在边BC,CD上),设 .
.

(Ⅰ)用t表示出PQ的长度,并探求 的周长l是否为定值;
的周长l是否为定值;
(Ⅱ)问探照灯照射在正方形ABCD内部区域阴影部分的面积S最大为多少(平方百米)?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)已知向量 ,
, ,设函数
,设函数
 的图象关于直线
的图象关于直线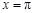 对称,其中
对称,其中 ,
, 为常数,且
为常数,且 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)若 的图象经过点
的图象经过点 ,求函数
,求函数 在区间
在区间 上的取值范围.
上的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com