
【题目】如图,在四面体![]() 中,
中,![]() ,
,![]() .
.
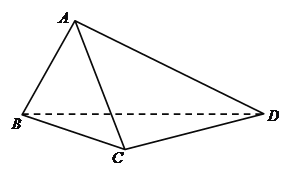
(1)证明:![]() ;
;
(2)若![]() ,
,![]() ,四面体
,四面体![]() 的体积为2,证明:平面
的体积为2,证明:平面![]() 平面
平面![]() .
.
【答案】(1)见解析;(2)见解析
【解析】分析:方法1:(1)作Rt△![]() 斜边
斜边![]() 上的高
上的高![]() ,连
,连![]() ,可得Rt△
,可得Rt△![]() ≌ Rt△
≌ Rt△![]() ,于是
,于是![]() ,由此可得
,由此可得![]() 平面
平面![]() ,于是
,于是![]() .(2)由题意得
.(2)由题意得![]() ,
,
然后根据![]() 平面
平面![]() ,四面体
,四面体![]() 的体积
的体积![]() 可得
可得![]() ,于是得到
,于是得到
![]() ,故
,故![]() ,所以得
,所以得![]() 平面
平面![]() ,由面面垂直的判定定理可得结论.
,由面面垂直的判定定理可得结论.
方法2:(1)由三角形全等可得![]() .取
.取![]() 的中点
的中点![]() ,连
,连![]() ,
,![]() ,则有
,则有![]() 平面
平面![]() ,从而可得
,从而可得![]() .(2)由题意得△
.(2)由题意得△![]() 面积为
面积为![]() ,根据
,根据![]() 可得点
可得点![]() 到平面
到平面![]() 距离
距离![]() .然后在平面
.然后在平面![]() 内过
内过![]() 作
作![]() 于
于![]() ,求得
,求得![]() .
.
故得![]() 平面
平面![]() ,可证得平面
,可证得平面![]() 平面
平面![]() .
.
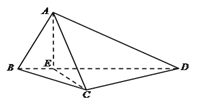
详解:(1)解法1:如图,作Rt△![]() 斜边
斜边![]() 上的高
上的高![]() ,连
,连![]() .
.
∵![]() ,
,![]() ,
,
∴Rt△![]() ≌ Rt△
≌ Rt△![]() .
.
于是可得![]() .
.
又![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() .
.
(2)在Rt△![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
, ![]() ,
,
△![]() 的面积
的面积![]() .
.
又![]() 平面
平面![]() ,四面体
,四面体![]() 的体积
的体积![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
解法2:
(1)∵![]() ,
,![]() ,
,
∴Rt△![]() ≌Rt△
≌Rt△![]() .
.
∴![]() .
.
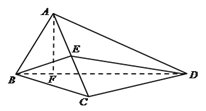
取![]() 的中点
的中点![]() ,连
,连![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
又![]()
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() .
.
(2)在Rt△![]() 中,
中,![]() ,
,![]() ,
,
∴△![]() 面积为
面积为![]() .
.
设![]() 到平面
到平面![]() 距离为
距离为![]() ,
,
则![]() ,
,
∴![]() .
.
在平面![]() 内过
内过![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() .
.
由点到平面距离定义知![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】有甲、乙两队学生参加“知识联想”抢答赛,比赛规则:①主持人依次给出两次提示,第一次提示后答对得2分,第二次提示后答对得1分,没抢到或答错者不得分;②主持人给出第一个提示后开始抢答,第一轮抢答出错失去第二轮答题资格;③每局比赛分两轮,若第一轮抢答者给出正确答案,则此局比赛结束,若第一轮答题者答错,主持人提示后另一队直接答题。如果甲、乙两队抢到答题权机会均等,并且势均力敌,第一个提示后答对概率均为![]() ;第二个提示后答对概率均为
;第二个提示后答对概率均为![]() ,
,![]() 为甲队在一局比赛中的分.
为甲队在一局比赛中的分.
(1)求甲在一局比赛中得分的分布列;
(2)若比赛共4局,求甲4局比赛中至少得6分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场销售某种商品的经验表明,该商品每日的销售量![]() (单位:千克)与销售价格
(单位:千克)与销售价格![]() (单位:元/千克)满足
(单位:元/千克)满足![]() ,其中
,其中![]() ,
,![]() 为常数.已知销售价格为7元/千克时,每日可售出该商品11千克.
为常数.已知销售价格为7元/千克时,每日可售出该商品11千克.
(1)求![]() 的值;
的值;
(2)若该商品成本为5元/千克,试确定销售价格![]() 值,使商场每日销售该商品所获利润最大.
值,使商场每日销售该商品所获利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解人们对“2019年3月在北京召开的第十三届全国人民代表大会第二次会议和政协第十三届全国委员会第二次会议”的关注度,某部门从年龄在15岁到65岁的人群中随机调查了100人,并得到如图所示的年龄频率分布直方图,在这100人中关注度非常髙的人数与年龄的统计结果如右表所示:

年龄 | 关注度非常高的人数 |
| 15 |
| 5 |
| 15 |
| 23 |
| 17 |
(Ⅰ)由频率分布直方图,估计这100人年龄的中位数和平均数;
(Ⅱ)根据以上统计数据填写下面的![]() 列联表,据此表,能否在犯错误的概率不超过
列联表,据此表,能否在犯错误的概率不超过![]() 的前提下,认为以45岁为分界点的不同人群对“两会”的关注度存在差异?
的前提下,认为以45岁为分界点的不同人群对“两会”的关注度存在差异?
(Ⅲ)按照分层抽样的方法从年龄在35岁以下的人中任选六人,再从六人中随机选两人,求两人中恰有一人年龄在25岁以下的概率是多少.
45岁以下 | 45岁以上 | 总计 | |
非常髙 | |||
一般 | |||
总计 |
参考数据:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,点
中,点![]() 在平面
在平面![]() 内运动,使得二面角
内运动,使得二面角![]() 的平面角与二面角
的平面角与二面角![]() 的平面角互余,则点
的平面角互余,则点![]() 的轨迹是( )
的轨迹是( )

A. 一段圆弧 B. 椭圆的一部分 C. 抛物线 D. 双曲线的一支
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阿基米德是古希腊伟大的哲学家、数学家、物理学家,对几何学、力学等学科作出过卓越贡献.为调查中学生对这一伟大科学家的了解程度,某调查小组随机抽取了某市的100名高中生,请他们列举阿基米德的成就,把能列举阿基米德成就不少于3项的称为“比较了解”,少于三项的称为“不太了解”.他们的调查结果如下:
0项 | 1项 | 2项 | 3项 | 4项 | 5项 | 5项以上 | |
理科生(人) | 1 | 10 | 17 | 14 | 14 | 10 | 4 |
文科生(人) | 0 | 8 | 10 | 6 | 3 | 2 | 1 |
(1)完成如下![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为,了解阿基米德与选择文理科有关?
的把握认为,了解阿基米德与选择文理科有关?
比较了解 | 不太了解 | 合计 | |
理科生 | |||
文科生 | |||
合计 |
(2)在抽取的100名高中生中,按照文理科采用分层抽样的方法抽取10人的样本.
(i)求抽取的文科生和理科生的人数;
(ii)从10人的样本中随机抽取3人,用![]() 表示这3人中文科生的人数,求
表示这3人中文科生的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
, ![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学只有两位说的话是对的,则获得一等奖的作品是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com