
【题目】已知函数f(x)=log22x﹣mlog2x+2,其中m∈R.
(1)当m=3时,求方程f(x)=0的解;
(2)当x∈[1,2]时,求f(x)的最小值.
【答案】
(1)解:令t=log2x,则当m=3时,方程f(x)=0可化为:t2﹣3t+2=0,解得:t=1或t=2
所以x=2或x=4
(2)解:令t=log2x,x∈[1,2],
则t∈[0,1],y=t2﹣mt+2,
其图象开口朝上,且以直线x= ![]() 为对称轴;
为对称轴;
①当 ![]() <0,即m=0时,
<0,即m=0时,
则t=0,即x=1时,f(x)min=2;
②当0≤ ![]() ≤1,即0≤m≤2时,
≤1,即0≤m≤2时,
则t=m,即x=2m时,f(x)min= ![]() +2;
+2;
③当 ![]() >1,即m>2时,
>1,即m>2时,
则t=1,即m=2时,f(x)min=3﹣m;
综上f(x)min= 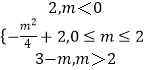
【解析】(1)令t=log2x,则当m=3时,方程f(x)=0可化为:t2﹣3t+2=0,解得答案;(2)令t=log2x,x∈[1,2],则t∈[0,1],y=t2﹣mt+2,结合二次函数的图象和性质,可得答案.
【考点精析】关于本题考查的二次函数的性质和二次函数在闭区间上的最值,需要了解当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减;当
上递减;当![]() 时,当
时,当![]() 时,
时,![]() ;当
;当![]() 时在
时在![]() 上递减,当
上递减,当![]() 时,
时,![]() 才能得出正确答案.
才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的上、下焦点分别为
的上、下焦点分别为![]() ,上焦点
,上焦点![]() 到直线 4x+3y+12=0的距离为3,椭圆C的离心率e=
到直线 4x+3y+12=0的距离为3,椭圆C的离心率e=![]() .
.
(I)若P是椭圆C上任意一点,求![]() 的取值范围;
的取值范围;
(II)设过椭圆C的上顶点A的直线![]() 与椭圆交于点B(B不在y轴上),垂直于
与椭圆交于点B(B不在y轴上),垂直于![]() 的直线与
的直线与![]() 交于点M,与
交于点M,与![]() 轴交于点H,若
轴交于点H,若![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 的左右焦点,
的左右焦点,![]() 为原点,
为原点,![]()
![]() 在椭圆上,线段
在椭圆上,线段![]() 与
与![]() 轴的交点
轴的交点![]() 满足
满足![]() .
.
(1)求椭圆的标准方程;
(2)过椭圆右焦点![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() 两点,交
两点,交![]() 轴于
轴于![]() 点,若
点,若![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2bx+5(b∈R).
(1)若b=2,试解不等式f(x)<10;
(2)若f(x)在区间[﹣4,﹣2]上的最小值为﹣11,试求b的值;
(3)若|f(x)﹣5|≤1在区间(0,1)上恒成立,试求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家拟在2017年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)![]() (单位:万件)与年促销费用
(单位:万件)与年促销费用![]() (单位:万元)(
(单位:万元)(![]() )满足
)满足![]() (
(![]() 为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2017年生产该产品的固定投入为8万元.每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2017年生产该产品的固定投入为8万元.每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将2017年该产品的利润![]() (单位:万元)表示为年促销费用
(单位:万元)表示为年促销费用![]() (单位:万元)的函数;
(单位:万元)的函数;
(2)该厂家2017年的促销费用投入多少万元时,厂家的利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com