
【题目】(本小题满分14分)
已知函数![]() (
(![]() 为常数)的图像与
为常数)的图像与![]() 轴交于点
轴交于点![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() .
.
(1)求![]() 的值及函数
的值及函数![]() 的极值;
的极值;
(2)证明:当![]() 时,
时,![]()
(3)证明:对任意给定的正数![]() ,总存在
,总存在![]() ,使得当
,使得当![]() 时,恒有
时,恒有![]()
【答案】(1)当![]() 时,
时,![]() 有极小值
有极小值![]() ,
,![]() 无极大值.
无极大值.
(2)见解析.(3)见解析.
【解析】
试题分析:(1)由![]() ,得
,得![]() .
.
从而![]() .
.
令![]() ,得驻点
,得驻点![]() .讨论可知:
.讨论可知:
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
当![]() 时,
时,![]() 有极小值
有极小值![]() ,
,![]() 无极大值.
无极大值.
(2)令![]() ,则
,则![]() .
.
根据![]() ,知
,知![]() 在R上单调递增,又
在R上单调递增,又![]() ,
,
当![]() 时,由
时,由![]() ,即得.
,即得.
(3)思路一:对任意给定的正数c,取![]() ,
,
根据![]() .得到当
.得到当![]() 时,
时,![]() .
.
思路二:令![]() ,转化得到只需
,转化得到只需![]() 成立.
成立.
分![]() ,
,![]() ,应用导数研究
,应用导数研究![]() 的单调性.
的单调性.
思路三:就①![]() ,②
,②![]() ,加以讨论.
,加以讨论.
试题解析:解法一:
(1)由![]() ,得
,得![]() .
.
又![]() ,得
,得![]() .
.
所以![]() ,
,![]() .
.
令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
所以当![]() 时,
时,![]() 有极小值,
有极小值,
且极小值为![]() ,
,
![]() 无极大值.
无极大值.
(2)令![]() ,则
,则![]() .
.
由(1)得,![]() ,即
,即![]() .
.
所以![]() 在R上单调递增,又
在R上单调递增,又![]() ,
,
所以当![]() 时,
时,![]() ,即
,即![]() .
.
(3)对任意给定的正数c,取![]() ,
,
由(2)知,当![]() 时,
时,![]() .
.
所以当![]() 时,
时,![]() ,即
,即![]() .
.
因此,对任意给定的正数c,总存在![]() ,当
,当![]() 时,恒有
时,恒有![]() .
.
解法二:(1)同解法一.
(2)同解法一.
(3)令![]() ,要使不等式
,要使不等式![]() 成立,只要
成立,只要![]() 成立.
成立.
而要使![]() 成立,则只需
成立,则只需![]() ,即
,即![]() 成立.
成立.
①若![]() ,则
,则![]() ,易知当
,易知当![]() 时,
时,![]() 成立.
成立.
即对任意![]() ,取
,取![]() ,当
,当![]() 时,恒有
时,恒有![]() .
.
②若![]() ,令
,令![]() ,则
,则![]() ,
,
所以当![]() 时,
时,![]() ,
,![]() 在
在![]() 内单调递增.
内单调递增.
取![]() ,
,
![]() ,
,
易知![]() ,
,![]() ,所以
,所以![]() .
.
因此对任意![]() ,取
,取![]() ,当
,当![]() 时,恒有
时,恒有![]() .
.
综上,对任意给定的正数c,总存在![]() ,当
,当![]() 时,恒有
时,恒有![]() .
.
解法三:(1)同解法一.
(2)同解法一.
(3)①若![]() ,取
,取![]() ,
,
由(2)的证明过程知,![]() ,
,
所以当![]() 时,有
时,有![]() ,即
,即![]() .
.
②若![]() ,
,
令![]() ,则
,则![]() ,
,
令![]() 得
得![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
取![]() ,
,
![]() ,
,
易知![]() ,又
,又![]() 在
在![]() 内单调递增,
内单调递增,
所以当![]() 时,恒有
时,恒有![]() ,即
,即![]() .
.
综上,对任意给定的正数c,总存在![]() ,当
,当![]() 时,恒有
时,恒有![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 图象上点
图象上点![]() 处的切线方程与直线
处的切线方程与直线![]() 平行(其中
平行(其中![]() ),
),![]() .
.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)求函数![]() 在
在![]() (
(![]() )上的最小值;
)上的最小值;
(Ⅲ)对一切![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为自然对数的底数,
为自然对数的底数,![]() ),
),![]() (
(![]() ,
,![]()
![]() ),
),
⑴若![]() ,
,![]() .求
.求![]() 在
在![]() 上的最大值
上的最大值![]() 的表达式;
的表达式;
⑵若![]() 时,方程
时,方程![]() 在
在![]() 上恰有两个相异实根,求实根
上恰有两个相异实根,求实根![]() 的取值范围;
的取值范围;
⑶若![]() ,
,![]() ,求使
,求使![]() 得图像恒在
得图像恒在![]() 图像上方的最大正整数
图像上方的最大正整数![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 越大,说明“
越大,说明“![]() 与
与![]() 有关系”的可信度越大.
有关系”的可信度越大.
②以模型![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设![]() ,将其变换后得到线性方程
,将其变换后得到线性方程![]() ,则
,则![]() 的值分别是
的值分别是![]() 和0.3.
和0.3.
③根据具有线性相关关系的两个变量的统计数据所得的回归直线方程为![]() 中,
中, ![]() ,
,
则![]() .正确的个数是( )
.正确的个数是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() ﹥
﹥![]() ﹥0)的离心率为
﹥0)的离心率为![]() ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,坐标原点
两点,坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数对![]() 一切实数
一切实数![]() 都有
都有![]() ,且当
,且当![]() 时,
时,![]() ,又
,又![]() .
.
(1)判断该函数的奇偶性并说明理由;、
(2)试判断该函数在![]() 上的单调性;
上的单调性;
(3)求![]() 在区间
在区间![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 是边长为4的正方形,点
是边长为4的正方形,点![]() 为
为![]() 边上任意一点(与点
边上任意一点(与点![]() 不重合),连接
不重合),连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,设
,设![]() .
.
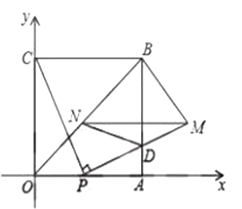
(1)求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示)
的代数式表示)
(2)试判断线段![]() 的长度是否随点
的长度是否随点![]() 的位置的变化而改变?并说明理由.
的位置的变化而改变?并说明理由.
(3)当![]() 为何值时,四边形
为何值时,四边形![]() 的面积最小.
的面积最小.
(4)在![]() 轴正半轴上存在点
轴正半轴上存在点![]() ,使得
,使得![]() 是等腰三角形,请直接写出不少于4个符合条件的点
是等腰三角形,请直接写出不少于4个符合条件的点![]() 的坐标(用含
的坐标(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为正常数.
为正常数.
⑴若![]() ,且
,且![]() ,求函数
,求函数![]() 的单调增区间;
的单调增区间;
⑵在⑴中当![]() 时,函数
时,函数![]() 的图象上任意不同的两点
的图象上任意不同的两点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() ,试证明:
,试证明: ![]() .
.
⑶若![]() ,且对任意的
,且对任意的![]() ,
, ![]() ,都有
,都有![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com