
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,且点
,且点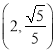 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,在直线
两点,在直线![]() 上存在点
上存在点![]() ,使三角形
,使三角形![]() 为正三角形,求
为正三角形,求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由离心率得![]() ,再把已知点的坐标代入椭圆方程,结合
,再把已知点的坐标代入椭圆方程,结合![]() 可解得
可解得![]() ,得椭圆方程;
,得椭圆方程;
(2)设直线![]() 方程为
方程为![]() ,与
,与![]() 联立方程组,消去
联立方程组,消去![]() ,设
,设![]() ,
,![]() ,由韦达定理得
,由韦达定理得![]()
![]() .设线段
.设线段![]() 的中点为
的中点为![]() ,得直线
,得直线![]() 方程,求出
方程,求出![]() 点坐标(此结论对
点坐标(此结论对![]() 也适用),
也适用),![]() 是等边三角形等价于
是等边三角形等价于![]() ,由此可把
,由此可把![]() 用
用![]() 表示,设
表示,设![]() 换元后,可利用基本不等式求得最值.
换元后,可利用基本不等式求得最值.
(1)设![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
由点 在椭圆
在椭圆![]() 上得
上得![]() ,
,
![]() ,
,![]() ,所以椭圆
,所以椭圆![]() 的方程为
的方程为![]() .
.
(2)显然,直线![]() 的斜率存在,设其方程为
的斜率存在,设其方程为![]() ,
,
与![]() 联立方程组,消去
联立方程组,消去![]() ,并化简得
,并化简得![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
设线段![]() 的中点为
的中点为![]() ,则直线
,则直线![]() :
:![]() ,令
,令![]() ,
,
又![]() ,得点
,得点![]() 的坐标为
的坐标为![]() ,显然当
,显然当![]() 时也符合,
时也符合,
所以![]() .
.
又因为![]() ,
,
由三角形![]() 为正三角形得
为正三角形得![]() ,
,
所以![]() 两边平方可得
两边平方可得
 ,得
,得 .
.
令![]() ,则
,则 ,当且仅当
,当且仅当![]() ,即
,即![]() 时等号成立,此时
时等号成立,此时![]() ,所以
,所以![]() 的最大值为
的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为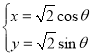 (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为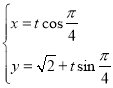 (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求曲线![]() 与曲线
与曲线![]() 的公共点的极坐标;
的公共点的极坐标;
(2)若点![]() 的极坐标为
的极坐标为![]() ,设曲线
,设曲线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,则在曲线
,则在曲线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ,若存在,求出点
,若存在,求出点![]() 的直角坐标,若不存在,请说明理由.
的直角坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科研团队对![]() 例新冠肺炎确诊患者的临床特征进行了回顾性分析.其中
例新冠肺炎确诊患者的临床特征进行了回顾性分析.其中![]() 名吸烟患者中,重症人数为
名吸烟患者中,重症人数为![]() 人,重症比例约为
人,重症比例约为![]() ;
;![]() 名非吸烟患者中,重症人数为
名非吸烟患者中,重症人数为![]() 人,重症比例为
人,重症比例为![]() .
.
(1)根据以上数据完成![]() 列联表;
列联表;
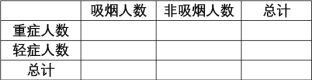
(2)根据(1)中列联表数据,能否在犯错误的概率不超过![]() 的前提下认为新冠肺炎重症与吸烟有关?
的前提下认为新冠肺炎重症与吸烟有关?
(3)已知每例重症患者平均治疗费用约为![]() 万元,每例轻症患者平均治疗费用约为
万元,每例轻症患者平均治疗费用约为![]() 万元.根据(1)中列联表数据,分别求吸烟患者和非吸烟患者的平均治疗费用.(结果保留两位小数)
万元.根据(1)中列联表数据,分别求吸烟患者和非吸烟患者的平均治疗费用.(结果保留两位小数)
附:
|
|
|
|
|
|
|
|
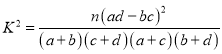
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,M,N,P分别是C1D1,BC,A1D1的中点,有下列四个结论:
①AP与CM是异面直线;②AP,CM,DD1相交于一点;③MN∥BD1;
④MN∥平面BB1D1D.
其中所有正确结论的编号是( )

A.①④B.②④C.①④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
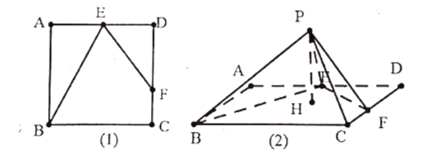
【题目】如图,边长为4的正方形![]() ,
,![]() 为
为![]() 中点,
中点,![]() 为
为![]() 边上一动点,现将
边上一动点,现将![]() ,
,![]() 分别沿
分别沿![]() ,
,![]() 折起,使得
折起,使得![]() ,
,![]() 重合为点
重合为点![]() ,形成四棱锥
,形成四棱锥![]() ,过点
,过点![]() 作
作![]() 平面
平面![]() 于
于![]() .①平面
.①平面![]() 平面
平面![]() ;②当
;②当![]() 为
为![]() 中点时,三棱锥
中点时,三棱锥![]() 的体积为
的体积为![]() ;③
;③![]() 为
为![]() 的垂心;④
的垂心;④![]() 长的取值范围为
长的取值范围为![]() .则以上判断正确的有______(填正确命题的序号).
.则以上判断正确的有______(填正确命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某晚会上某歌舞节目的表演者是3个女孩和4个男孩.演出结束后,7个人合影留念(3个人站在前排,4个人站在后排),其中男孩甲、乙要求站在一起,女孩丙不能站在两边,不同站法的种数为( )
A.96B.240C.288D.432
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1为某省2018年1~4月快递业务量统计图,图2是该省2018年1~4月快递业务收入统计图,下列对统计图理解错误的是( )


A. 2018年1~4月的业务量,3月最高,2月最低,差值接近2000万件
B. 2018年1~4月的业务量同比增长率均超过50%,在3月底最高
C. 从两图来看,2018年1~4月中的同一个月的快递业务量与收入的同比增长率并不完全一致
D. 从1~4月来看,该省在2018年快递业务收入同比增长率逐月增长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com