练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    数列的前项和____________.
    解：因为数列，则通项公式
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：单选题

    设数列的前n项和，则的值为（  ）
    A．15B．16C．49D．64

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分12分）
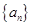
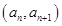
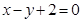
    已知数列的首项为2，点在函数的图像上
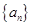
    （Ⅰ）求数列的通项公式；
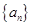
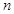
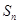
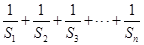
    （Ⅱ）设数列的前项之和为，求的值．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

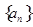
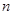
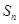
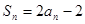
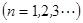
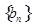
    (本小题满分14分) 已知数列的前项和为，且，等差数列中，，。
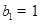
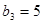
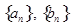
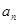
    （1）求数列的通项和；
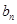
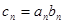
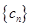
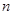
    (2) 设，求数列的前项和，

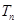
    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

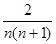
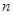
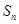
    已知数列{an }的通项公式为an=,则数列{an }的前项和为
    ____________;

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分14分）
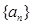
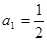
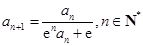
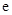
    已知数列满足：，（其中为自然对数的底数）．
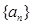
    （1）求数列的通项；
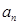
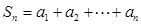
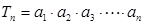
    （2）设，，求证：， ．

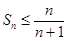
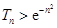
    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    化简的结果是（   ）
    A．B．
    C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

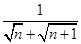
    数列{an}的通项公式an＝，若前n项的和为10，则项数n为_____．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    数列的前n项和为，且数列的各项按如下规则排列：

    则=       ，若存在正整数k，使，则k=          。

    查看答案和解析>>

    同步练习册答案