
分析 把要解的不等式等价转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.
解答 解:不等式|2x+1|-|x-4|<6等价于 $\left\{\begin{array}{l}{x<-\frac{1}{2}}\\{-2x-1-(4-x)<6}\end{array}\right.$①,或 $\left\{\begin{array}{l}{-\frac{1}{2}≤x≤4}\\{2x+1-(4-x)<6}\end{array}\right.$②,或$\left\{\begin{array}{l}{x>4}\\{2x+1-(x-4)<6}\end{array}\right.$③,
解①求得-11<x<-$\frac{1}{2}$,解②求得-$\frac{1}{2}$≤x<3,解③求得x∈∅.
综上可得,原不等式的解集为{x|-11<x<3},
故答案为:(-11,3).
点评 本题主要考查绝对值不等式的解法,体现了等价转化和分类讨论的数学思想,属于基础题.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直角梯形ABCD中,∠BAD=∠ADC=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=2a.
如图,在直角梯形ABCD中,∠BAD=∠ADC=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=2a.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 35 | B. | 70 | C. | 80 | D. | 140 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
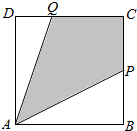 如图,有一块边长为1(百米)的正方形区域ABCD.在点A处有一个可转动的探照灯,其照射角∠PAQ始终为45°(其中点P,Q分别在边BC,CD上),设BP=t.
如图,有一块边长为1(百米)的正方形区域ABCD.在点A处有一个可转动的探照灯,其照射角∠PAQ始终为45°(其中点P,Q分别在边BC,CD上),设BP=t.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com