
 如图,在四棱锥A-BCDE中,底面BCDE为矩形,AB=AC,BC=2,CD=1,并且侧面ABC⊥底面BCDE.
如图,在四棱锥A-BCDE中,底面BCDE为矩形,AB=AC,BC=2,CD=1,并且侧面ABC⊥底面BCDE. 证明:(1)取AB的中点为P,连PC,PG,
证明:(1)取AB的中点为P,连PC,PG,
 BE,又CF
BE,又CF
 BE
BE

 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:
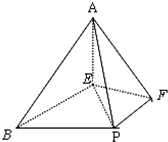 如图,在四棱锥A-BEFP中,AE⊥底面BEFP,BE⊥EF,∠EBP=
如图,在四棱锥A-BEFP中,AE⊥底面BEFP,BE⊥EF,∠EBP=| π | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
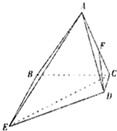 (2013•石家庄二模)如图,在四棱锥A-BCDE中,底面BCDE为直角梯形,且BE∥CD,CD⊥BC.侧面ABC⊥底面BCDE,F为AC的中点,BC=BE=4CD=2,AB=AC.
(2013•石家庄二模)如图,在四棱锥A-BCDE中,底面BCDE为直角梯形,且BE∥CD,CD⊥BC.侧面ABC⊥底面BCDE,F为AC的中点,BC=BE=4CD=2,AB=AC.| 3 |
查看答案和解析>>
科目:高中数学 来源:2014届河南省毕业班阶段测试一理数学卷(解析版) 题型:解答题
如图,在四棱锥A-BCDE中,底面四边形BCDE是等腰梯形,BC∥DE, =45
=45 ,O是BC的中点,AO=
,O是BC的中点,AO= ,且BC=6,AD=AE=2CD=2
,且BC=6,AD=AE=2CD=2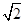 ,
,
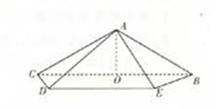
(1)证明:AO⊥平面BCD;(2)求二面角A-CD-B的平面角的正切值.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省中山市纪念中学高三(上)9月月考数学试卷(理科)(解析版) 题型:解答题
 ,AE=1,BE=FA=PB=2.
,AE=1,BE=FA=PB=2.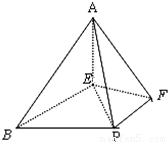
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省中山市纪念中学高三(上)9月月考数学试卷(理科)(解析版) 题型:解答题
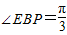 ,AE=1,BE=FA=PB=2.
,AE=1,BE=FA=PB=2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com