
【题目】已知函数f(x)=(ax﹣1)ex(a≠0,e是自然对数的底数).
(1)若函数f(x)在区间[1,2]上是单调减函数,求实数a的取值范围;
(2)求函数f(x)的极值;
(3)设函数f(x)图象上任意一点处的切线为l,求l在x轴上的截距的取值范围.
【答案】
(1)解:函数f(x)的导函数f'(x)=(ax﹣1+a)ex,
则f'(x)≤0在区间[1,2]上恒成立,且等号不恒成立,
又ex>0,所以ax﹣1+a≤0在区间[1,2]上恒成立,
记g(x)=ax﹣1+a,只需 ![]() ,即
,即 ![]() ,解得
,解得 ![]() 且a≠0
且a≠0
(2)解:由f'(x)=(ax﹣1+a)ex=0,得 ![]() ,
,
①当a<0时,有 ![]() ;
; ![]() ,
,
所以函数f(x)在 ![]() 单调递增,
单调递增, ![]() 单调递减,
单调递减,
所以函数f(x)在 ![]() 取得极大值
取得极大值 ![]() ,没有极小值.
,没有极小值.
②当a>0时,有 ![]() ;
; ![]() ,
,
所以函数f(x)在 ![]() 单调递减,
单调递减, ![]() 单调递增,
单调递增,
所以函数f(x)在 ![]() 取得极小值
取得极小值 ![]() ,没有极大值.
,没有极大值.
综上可知:当a<0时,函数f(x)在 ![]() 取得极大值
取得极大值 ![]() ,没有极小值;
,没有极小值;
当a>0时,函数f(x)在 ![]() 取得极小值
取得极小值 ![]() ,没有极大值
,没有极大值
(3)解:设切点为T(t,(at﹣1)et),
则曲线在点T处的切线l方程为y﹣(at﹣1)et=(at﹣1+a)(x﹣t)et,
当 ![]() 时,切线l的方程为
时,切线l的方程为 ![]() ,其在x轴上的截距不存在.
,其在x轴上的截距不存在.
当 ![]() 时,令y=0,得切线l在x轴上的截距为:
时,令y=0,得切线l在x轴上的截距为:
![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() ,…(12分)
,…(12分)
当 ![]() 时,
时, 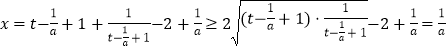 ,
,
当且仅当 ![]() ,即
,即 ![]() 或
或 ![]() 时取等号
时取等号
当 ![]() 时,
时,  ,
,
当且仅当 ![]() ,即
,即 ![]() 或
或 ![]() 时取等号.
时取等号.
所以切线l在x轴上的截距范围是 ![]()
【解析】(1)根据已知可判断函数极值的情况,先找导数为零的点,再判断导数为零的点的左、右两侧的导数符号。(2)根据已知函数求极值求f'(x),令f'(x)=0的求出根并列表检验f'(x)在f'(x)=0的根的附近两侧的符号进而得到结果。(3)利用已知极值求参数,若函数f(x)在点![]() 极值处取得极值,则f'(x)=0,且在该点左右两侧的导数值符号相反。,进而得出切线l在x轴上的截距范围。
极值处取得极值,则f'(x)=0,且在该点左右两侧的导数值符号相反。,进而得出切线l在x轴上的截距范围。
【考点精析】认真审题,首先需要了解函数的最大(小)值与导数(求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值).
比较,其中最大的是一个最大值,最小的是最小值).


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】如图中的三个直角三角形是一个体积为20cm3的几何体的三视图,则该几何体外接球的面积(单位:cm2)等于( )
A.55π
B.75π
C.77π
D.65π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年射阳县洋马镇政府决定投资8千万元启动“鹤乡菊海”观光旅游及菊花产业项目.规划从2017年起,在相当长的年份里,每年继续投资2千万元用于此项目.2016年该项目的净收入为5百万元(含旅游净收入与菊花产业净收入),并预测在相当长的年份里,每年的净收入均为上一年的1.5倍.记2016年为第1年,f(n)为第1年至此后第n(n∈N*)年的累计利润(注:含第n年,累计利润=累计净收入﹣累计投入,单位:千万元),且当f(n)为正值时,认为该项目赢利.
(1)试求f(n)的表达式;
(2)根据预测,该项目将从哪一年开始并持续赢利?请说明理由.
(参考数据: ![]() ,ln2≈0.7,ln3≈1.1)
,ln2≈0.7,ln3≈1.1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C所对的边分别为a,b,c且a+2c=2bcosA.
(1)求角B的大小;
(2)若b=2 ![]() ,a+c=4,求△ABC的面积.
,a+c=4,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC所在的平面内,点P0、P满足 ![]() =
= ![]()
![]() ,
, ![]() ,且对于任意实数λ,恒有
,且对于任意实数λ,恒有 ![]()
![]() ,则( )
,则( )
A.∠ABC=90°
B.∠BAC=90°
C.AC=BC
D.AB=AC
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(x+θ)﹣cos ![]() cos(
cos( ![]() ﹣
﹣ ![]() )(其中A为常数,θ∈(﹣π,0),若实数x1 , x2 , x3满足;①x1<x2<x3 , ②x3﹣x1<2π,③f(x1)=f(x2)=f(x3),则θ的值为 .
)(其中A为常数,θ∈(﹣π,0),若实数x1 , x2 , x3满足;①x1<x2<x3 , ②x3﹣x1<2π,③f(x1)=f(x2)=f(x3),则θ的值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设n≥3,n∈N* , 在集合{1,2,…,n}的所有元素个数为2的子集中,把每个子集的较大元素相加,和记为a,较小元素之和记为b.
(1)当n=3时,求a,b的值;
(2)求证:对任意的n≥3,n∈N* , ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区拟建立一个艺术搏物馆,采取竞标的方式从多家建筑公司选取一家建筑公司,经过层层筛选,甲、乙两家建筑公司进入最后的招标.现从建筑设计院聘请专家设计了一个招标方案:两家公司从6个招标总是中随机抽取3个总题,已知这6个招标问题中,甲公司可正确回答其中4道题目,而乙公司能正面回答每道题目的概率均为 ![]() ,甲、乙两家公司对每题的回答都是相独立,互不影响的.
,甲、乙两家公司对每题的回答都是相独立,互不影响的.
(1)求甲、乙两家公司共答对2道题目的概率;
(2)请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com