
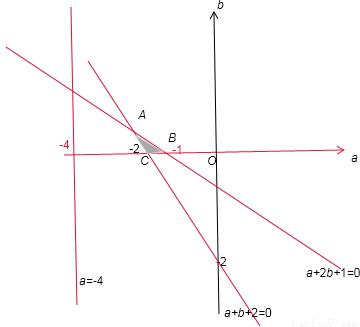
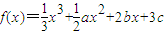 的两个极值点分别为x1,x2,且x1∈(0,1),x2∈(1,2),则b-3a的取值范围是( )
的两个极值点分别为x1,x2,且x1∈(0,1),x2∈(1,2),则b-3a的取值范围是( )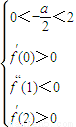 ,代入可得关于a,b的二元一次不等式组,利用线性规划的知识,画出平面区域,在可行域内找到目标函数=-3a+b取得最大值及最小值点.
,代入可得关于a,b的二元一次不等式组,利用线性规划的知识,画出平面区域,在可行域内找到目标函数=-3a+b取得最大值及最小值点.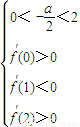 ,∴
,∴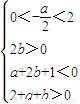 ,
,


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源:2013-2014学年湖南省三校高三上学期联考理科数学试卷(解析版) 题型:填空题
已知函数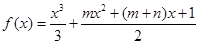 的两个极值点分别为
的两个极值点分别为 ,且
,且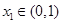 ,
,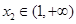 ,点
,点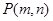 表示的平面区域为
表示的平面区域为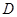 ,若函数
,若函数 的图象上存在区域
的图象上存在区域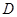 内的点,则实数
内的点,则实数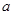 的取值范围为
.
的取值范围为
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省高三上学期四调考试理科数学试卷(解析版) 题型:选择题
已知函数 的两个极值点分别为
的两个极值点分别为 ,且
,且 ,
, ,点
,点 表示的平面区域为
表示的平面区域为 ,若函数
,若函数 的图像上存在区域
的图像上存在区域 内的点,则实数
内的点,则实数 的取值范围是( )
的取值范围是( )
A.  B.
B.
 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014届云南师大附中高考适应性月考理科数学试卷(一)(解析版) 题型:选择题
已知函数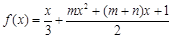 的两个极值点分别为
的两个极值点分别为 ,且
,且 ,
,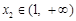 ,点
,点 表示的平面区域为
表示的平面区域为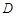 ,若函数
,若函数 的图像上存在区域
的图像上存在区域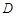 内的点,则实数的取值范围是( )
内的点,则实数的取值范围是( )
A. B.
B.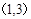 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年甘肃省高三第三次模拟考试理科数学试卷(解析版) 题型:选择题
已知函数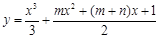 的两个极值点分别为x1,x2,且x1Î(0,
1),x2Î(1, +¥),记分别以m,n为横、纵坐标的点P(m,n)表示的平面区域为D,若函数
的两个极值点分别为x1,x2,且x1Î(0,
1),x2Î(1, +¥),记分别以m,n为横、纵坐标的点P(m,n)表示的平面区域为D,若函数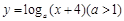 的图象上存在区域D内的点,则实数a的取值范围为(
)
的图象上存在区域D内的点,则实数a的取值范围为(
)
A.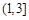 B.
B.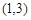 C.
C.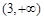 D.
D.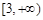
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com