
【题目】我市幸福社区在“9.9重阳节”向本社区征召100名义务宣传“敬老爱老”志愿者,现把该100名志愿者的成员按年龄分成5组,如下表所示:
组别 | 年龄 | 人数 |
1 |
| 10 |
2 |
| 30 |
3 |
| 20 |
4 |
| 30 |
5 |
| 10 |
(1)若从第1,2,3组中用分层抽样的方法选出6名志愿者参加某社区宣传活动,应从第1,2,3组各选出多少名志愿者?
(2)在(1)的条件下,宣传决定在这6名志愿者中随机选2名志愿者介绍宣传经验.
(i)列出所有可能的结果;
(ii)求第3组至少有1名志愿者被选中的概率.
【答案】(1)答案见解析;(2)(i)答案见解析;(2)![]() .
.
【解析】
(1)由题意利用分层抽样的定义和抽样比即可确定所需抽取的志愿者人数;
(2)首先列出所有可能的结果,然后结合列出的结果和对立事件概率公式即可求得满足题意的概率值.
(1)由题意结合分层抽样的定义可知:
第1组应抽取的人数为:![]() 人;
人;
第2组应抽取的人数为:![]() 人;
人;
第3组应抽取的人数为:![]() 人.
人.
(2)(i)设第1组的志愿者为a,第二组的志愿者为b,c,d,第三组的志愿者为e,f,
则所有可能的结果为:ab,ac,ad,ae,af,bc,bd,be,bf,cd,ce,cf,de,df,ef.
(ii)结合(i)中的结果可知共有15种可能的结果,其中不满足题意的结果为:ab,ac,ad,bc,bd,cd,共6种,
则第3组至少有1名志愿者被选中的概率![]() .
.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两焦点与短轴的一个端点的连线构成等腰直角三角形,
的两焦点与短轴的一个端点的连线构成等腰直角三角形,
直线![]() 与以椭圆C的右焦点为圆心,以椭圆的长半轴长为半径的圆相切.
与以椭圆C的右焦点为圆心,以椭圆的长半轴长为半径的圆相切.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设P为椭圆C上一点,若过点![]() 的直线
的直线![]() 与椭圆C相交于不同的两点S和T,
与椭圆C相交于不同的两点S和T,
满足![]() (O为坐标原点),求实数
(O为坐标原点),求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出如下四种说法:
①四个实数![]() 依次成等比数列的必要而不充分条件是
依次成等比数列的必要而不充分条件是![]() .
.
②命题“若![]() 且
且![]() ,则
,则![]() ”为假命题.
”为假命题.
③若![]() 为假命题,则
为假命题,则![]() 均为假命题.
均为假命题.
④若数列![]() 的前项n和
的前项n和![]() ,则该数列的通项公式
,则该数列的通项公式![]() .
.
其中正确说法的序号为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电动汽车“行车数据”的两次记录如下表:
记录时间 | 累计里程 (单位:公里) | 平均耗电量(单位: | 剩余续航里程 (单位:公里) |
2019年1月1日 | 4000 | 0.125 | 280 |
2019年1月2日 | 4100 | 0.126 | 146 |
(注:累计里程指汽车从出厂开始累计行驶的路程,累计耗电量指汽车从出厂开始累计消耗的电量,平均耗电量=![]() ,剩余续航里程=
,剩余续航里程=![]() ,下面对该车在两次记录时间段内行驶100公里的耗电量估计正确的是
,下面对该车在两次记录时间段内行驶100公里的耗电量估计正确的是
A. 等于12.5B. 12.5到12.6之间
C. 等于12.6D. 大于12.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将参加夏令营的600名学生编号为:001,002,…,600,采用系统抽样方法抽取一个容量为50的样本,且随机抽得的号码为003.这600名学生分住在三个营区,从001到200住在第一营区,从201到500住在第二营区,从501到600住在第三营区,三个营区被抽中的人数依次为( ).
A.16,26,8B.17,24,9C.16,25,9D.17,25,8
查看答案和解析>>
科目:高中数学 来源: 题型:
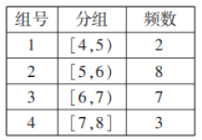
【题目】环境指数是“宜居城市”评比的重要指标.根据以下环境指数的数据,对名列前20名的“宜居城市”的环境指数进行分组统计,结果如表所示,现从环境指数在[4,5)和[7,8]内的“宜居城市”中随机抽取2个市进行调研,则至少有1个市的环境指数在[7,8]的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com